Regularization in Machine Learning¶

ក្នុងអត្ថបទមុនយើងបានស្វែងយល់អំពីម៉ូឌែលតម្រែតម្រង់លីនេអ៊ែរនិងវិធីសាស្រ្តក្នុងការកំណត់តម្លៃមេគុណតម្រែតម្រង់(ប៉ារ៉ាម៉ែត្រ)ដោយប្រើប្រាស់គណិតវិទ្យាវិភាគនិងវិធីសាស្រ្តប៉ាន់ស្មានតម្លៃតាមវិធីសាស្រ្តSGD។ ប៉ុន្តែបញ្ហាដែលនៅសល់គឺថាតើយើងគួរជ្រើសរើសយកម៉ូឌែលបែបណាទើបអាចឱ្យវាពណ៌នាទំនាក់ទំនងរវាងទិន្នន័យបានល្អប្រសើរ។ យើងពិនិត្យករណីខាងក្រោមជាឧទាហរណ៍។ សន្មតថាយើងមានទិន្នន័យដូចរូប(លើ)។ យើងចង់បង្កើតម៉ូឌែលតម្រែតម្រង់ដើម្បីសិក្សាពីទំនាក់ទំនងរវាងអថេរពន្យល់និងអថេរគោលដៅ។ ដើម្បីសិក្សាពីភាពល្អប្រសើរនៃម៉ូឌែល យើងបែងចែកទិន្នន័យជាពីរផ្នែកគឺ training data ដែលប្រើសម្រាប់កំណត់ប៉ារ៉ាម៉ែត្រក្នុងម៉ូឌែលនិង test data សម្រាប់ធ្វើការវាយតម្លៃ។

ក្នុងរូបខាងក្រោមបង្ហាញពីលទ្ធផលនៅពេលដែលយើងអនុវត្តម៉ូឌែលជាពហុធាដឺក្រេទី១(បន្ទាត់)និងពហុធាដឺក្រេខ្ពស់(ខែ្សកោង)។ យើងអាចពិនិត្យឃើញថា នៅពេលយើងជ្រើសយកម៉ូឌែលសាមញ្ញបំផុតពោលគឺបន្ទាត់ដឺក្រេទី១ នោះកម្រិតនៃការពណ៌នារបស់ម៉ូឌែលទៅលើទិន្នន័យ( Coefficient of determination: $R^2$)មានតម្លៃទាបដែលបង្ហាញថាមិនអាចពន្យល់បានល្អឡើយចំពោះទិន្នន័យដែលមាន។ ផ្ទុយទៅវិញ នៅពេលដែលយើងតម្លើងដឺក្រេនៃម៉ូឌែលកាន់តែខ្ពស់ យើងពិនិត្យឃើញថាតម្លៃនៃ$R^2$មានការកើនឡើងខ្លះដែលអាចឱ្យយើងនិយាយបានថាវាពន្យល់លើទំនាក់ទំនងរបស់ទិន្នន័យ បានប្រសើរ។ ប៉ុន្តែតើការតម្លើងម៉ូឌែលឱ្យកាន់តែស្មុគសម្មាញ(តម្លើងដឺក្រេ)វាពិតជាផ្តល់ឱ្យយើងនូវម៉ូឌែលដែលល្អមែនឬ?

reg1 reg2

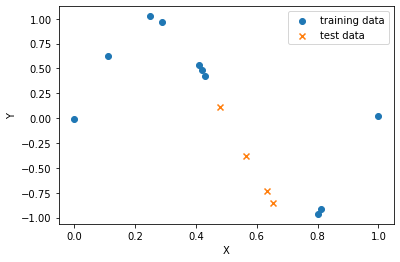
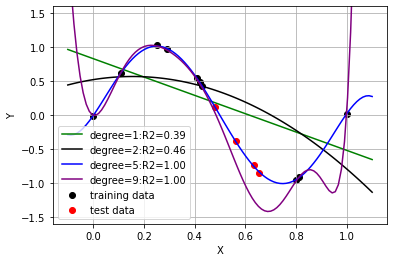
នៅក្នុងរូប(ក្រោម)បើយើងពិនិត្យលើទិន្នន័យដែលមិនត្រូវបានប្រើក្នុងការកំណត់តម្លៃមេគុណតម្រែតម្រង់(test data)នោះយើងឃើញថា ម៉ូឌែលដែលមានដឺក្រេលំដាប់ខ្ពស់ឬម៉ូឌែលដែលស្មុគស្មាញខ្លាំងមិនអាចប៉ាន់ស្មាន ឬពន្យល់ទំនាក់ទំនងរវាងអថេរពន្យល់និងអថេរគោលដៅបានល្អឡើយបើប្រៀបធៀបជាមួយម៉ូឌែលដែលមានដឺក្រេទាបជាងវា។ ហេតុនេះ តើយើងគួរធ្វើបែបណាដើម្បីជ្រើសបានម៉ូឌែលដែលអាចពន្យល់បានល្អទាំងចំពោះ ទិន្នន័យដែលប្រើក្នុងដំណាក់កាលកំណត់ប៉ារ៉ាម៉ែត្រ(learning) trainig data និងទាំងចំពោះទិន្នន័យដែលមិនត្រូវបានប្រើនៅដំណាក់កាលlearning(test data)?

Regularization¶

ដើម្បីដោះស្រាយបញ្ហានេះ Regularization ត្រូវបានប្រើប្រាស់។ ក្នុងវិធីសាស្រ្តនេះ ភាពស្មុគ ស្មាញនៃម៉ូឌែលត្រូវបានគិតគូររួមគ្នាជាមួយនិងតម្លៃនៃកម្រិតល្អៀងរបស់ម៉ូឌែល។ ឧទាហរណ៍ក្នុងករណីម៉ូឌែលតម្រែតម្រង់លីនេអ៊ែរដែលយើងបានសិក្សាកន្លងមកនេះ ការធ្វើបរមាកម្មលើតម្លៃលម្អៀងត្រូវបានផ្លាស់ប្តូរទៅជាទម្រង់$\ L\left(\pmb{\beta},\alpha\right)$ដូចខាងក្រោម ។ នៅទីនេះ ផ្នែក$\ R\left(\pmb{\beta}\right)$ គឺជាផ្នែកដែលបង្ហាញពីកម្រិតនៃភាពស្មុគស្មាញរបស់ម៉ូឌែល ហើយ$\alpha $ជាមេគុណដែលប្រើដើម្បីកម្រិតឥទ្ធិពលនៃ$\ R\left(\pmb{\beta}\right) $ពេលធ្វើបរមាកម្ម។

ម៉ូឌែល $$\pmb{y}=X\pmb{\beta}+\pmb{\epsilon}$$ L\left(\pmb{\beta},\alpha\right)=E\left(\pmb{\beta}\right)+\alpha R\left(\pmb{\beta}\right) $$

ផ្នែក$\ R\left(\pmb{\beta}\right) \left(\pmb{\beta}=\left(\beta_1,\ldots,\beta_d\right)^\top\right) $ ដែលបង្ហាញពីកម្រិតនៃភាពស្មុគស្មាញរបស់ម៉ូឌែលត្រូវបាន បង្ហាញជាទម្រង់នានាដូចជា $$ Ridge\ penalty\left(L2\ regularization\right)∶\ R\left(\pmb{\beta}\right)=||\beta||^2=\beta_1^2+\cdots+\beta_d^2 $$

\[L1\ regularization∶\ R\left(\pmb{\beta}\right)=\left|\beta_1+\ldots+\beta_d\right|\]

ក្នុងអត្ថបទនេះ យើងនឹងណែនាំអំពី L2 regularization ចំពោះម៉ូឌែលតម្រែតម្រង់ដែលហៅថា Ridge Regression Model។

Ridge Regression Model¶

នៅក្នុង Ridge Regression Model តម្លៃការេនៃណមរបស់វ៉ិចទ័រមេគុណតម្រែតម្រង់ ត្រូវបានប្រើប្រាស់សម្រាប់បង្ហាញពីកម្រិតស្មុគស្មាញរបស់ម៉ូឌែល។ ក្នុងករណីនេះ ដើម្បីកំណត់តម្លៃមេគុណតម្រែតម្រង់ យើងនឹងធ្វើអប្បបរមាកម្មលើ អនុគមន៍ដែលកំណត់ដូចខាងក្រោម។

\[L\left(\pmb{\beta},\alpha\right)=E\left(\pmb{\beta}\right)+\alpha R\left(\pmb{\beta}\right)=y-Xβ^{\top}y-Xβ+αβ^2\]

\[\hat{\pmb{\beta}} =\underset{\pmb{\beta}}{\arg\min}　{L\left(\pmb{\beta},\alpha\right)}\]

តាមរយៈការធ្វើបរមាកម្មបែបនេះ យើងនឹងអាចកំណត់បាននូវម៉ូឌែលដែលមានកម្រិត លម្អៀងតូចព្រមទាំងទំហំ នៃមេគុណតម្រែតម្រង់ (ដែលយើងសន្មតថាជាកម្រិតភាពស្មុគស្មាញក្នុងករណីនេះ) បានព្រមគ្នា។នៅទីនេះដើម្បីធ្វើតុល្យកម្មរវាងកម្រិតលម្អៀងរបស់ម៉ូឌែលនិងភាពស្មុគស្មាញ(ទំហំនៃមេគុណតម្រែតម្រង់)យើងអាចកែសម្រួលតម្លៃនៃមេគុណ$\ \alpha $បាន។

ដើម្បីដោះស្រាយបង្ហាញបរមាកម្មខាងលើ ដូចក្នុងអត្ថបទមុនៗដែរ យើងអាចដោះស្រាយតាមគណិតវិទ្យាវិភាគដោយធ្វើដេរីវេរួចរកតម្លៃនៃអថេរត្រង់ដេរីវេស្មើសូន្យ(ករណីអនុគមន៍ប៉ោង) ឬ ដោះស្រាយដោយប្រើវិធីសាស្រ្តSGD។

ចំពោះចម្លើយតាមគណិតវិទ្យាវិភាគ ទម្រង់នៃមេគុណតម្រែតម្រង់ត្រូវបានគណនាដូចខាងក្រោម(ដំណោះស្រាយទុកជាកិច្ចការផ្ទះជូនមិត្តអ្នកអាន) ដែល $I_d $ ជាម៉ាទ្រីសឯកតា។

\[\hat{\pmb{\beta}}=\left(X^\top X+\alpha I_d\right)^{-1}X^T\pmb{y}\]

ចំពោះចម្លើយតាមSGD ការផ្លាស់ប្តូរតម្លៃមេគុណតម្រែតម្រង់ត្រូវបានគណនាដូចខាងក្រោម(ដំណោះស្រាយទុកជាកិច្ចការផ្ទះជូនមិត្តអ្នកអាន) ដែល$N$ ជាចំនួនtraining data និង\eta_t ជា learing rate ។ $$ \pmb{\beta}^{\left(t+1\right)}=\left(1-\frac{2\alpha\eta_t}{N}\right)\pmb{\beta}^{\left(t\right)}-2\eta_t\left({{\hat{y}}_i}^{\left(t\right)}-y\right)\pmb{x}_i^\top $$

import numpy as np 
import matplotlib.pyplot as plt 

def ridge_fit(x,y,k,alpha):
  X_ = np.zeros((len(x),k+1))
  for i in range(k+1):
    X_[:,i] = x**i
  beta = np.linalg.inv(X_.T@X_+alpha*np.eye(k+1))@X_.T@y
  return beta

# learning with SGD
def ridge_sgd_fit(x,y,k,alpha):
  beta = np.zeros(k+1)
  d_index = list(range(len(x)))

  eta = 1e-4
  for t in range(500000):
    random.shuffle(d_index)
    for i in d_index :
      xi = np.zeros(k+1)
      for j in range(k+1):
        xi[j] = x[i]**j
      y_hat = xi.T @ beta
      beta = (1-2*alpha*eta/len(x))*beta - 2 * eta * (y_hat - y[i]) * xi
  return beta

def fit(x,y,k):
  X_ = np.zeros((len(x),k+1))
  for i in range(k+1):
    X_[:,i] = x**i
  w = np.linalg.inv(X_.T@X_)@X_.T@y
  return w

def predict(x,w,k):
    X_ = np.zeros((len(x),k+1))
    for i in range(k+1):
        X_[:,i] = x**i
    return X_@w

np.random.RandomState(0)
# Data: train
Xtrain = np.array([0.  ,  0.11,  0.25,  0.29,  0.41,  0.42,  0.43,  0.8 ,  0.81, 1.])
Ytrain = np.sin(2*np.pi*Xtrain)+0.02*np.random.randn(len(Xtrain))
# Data: test
Xtest = np.array([0.654,0.633,0.48,0.564])
Ytest = np.sin(2*np.pi*Xtest)+0.02*np.random.randn(len(Xtest))

markers = ['-','-']
alphas = [1e-9]
w_fit = []
d = 9
plt.scatter(Xtrain,Ytrain,marker='o',color='black')
plt.scatter(Xtest,Ytest,marker='o',color='red')
for i,alpha in enumerate(alphas):
  w = ridge_fit(Xtrain,Ytrain,d,alpha)
  #w = ridge_sgd_fit(Xtrain,Ytrain,d,alpha)
  w_fit.append(w)
  xa = np.linspace(min(Xtrain)-0.1,max(Xtrain)+0.1,100)
  ya = predict(xa,w,d)
  plt.plot(xa,ya,markers[i])
plt.grid()
plt.plot(xa,predict(xa,fit(Xtrain,Ytrain,d),d),'g-.')
plt.ylim([-1.6,1.6])
plt.legend(['Ridge Model with alpha='+str(i) for i in alphas]+['no regulization','training data','test data'])
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Linear Regression Model (Polynomial degree=9)')
plt.show()

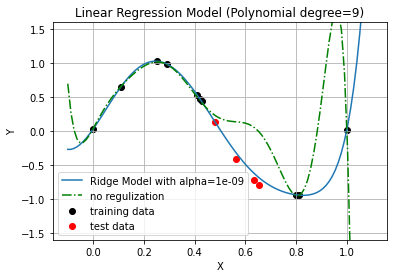
រូបខាងលើបង្ហាញពីលទ្ធផលនៅពេល L2 regularization ត្រូវបានប្រើលើម៉ូឌែលតម្រែតម្រង់ជាទម្រង់ពហុធាដឺក្រេទី៩។ យើងពិនិត្យឃើញថា នៅពេល regularization ត្រូវបានប្រើ ម៉ូឌែលអាចពន្យល់បានល្អទំាងចំពោះ training data និង test data ព្រមគ្នា ផ្ទុយពីម៉ូឌែលដែលមិនប្រើ regularization។

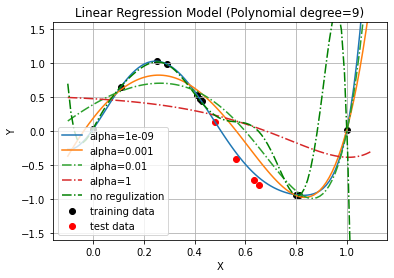
តាមពិតទៅយើងនៅសល់បញ្ហាមួយទៀតគឺការកំណត់តម្លៃនៃមេគុណ$\ \alpha\ $។ ដំណោះស្រាយក្នុងបញ្ហានេះអាចធ្វើបានតាមរយៈការសាកល្បងលើតម្លៃជាច្រើននៃ$\ \alpha\ $ចំពោះទិន្នន័យមួយផ្នែកដែលមិនមែនជាtest data , training data ដែលយើងហៅថា validation data ។ យើងអាចកំណត់តម្លៃ$\ \alpha\ $ដោយជ្រើសយកតម្លៃ$\ \alpha\ $ ណាដែលធ្វើឲ្យស្ថានភាពនៃម៉ូឌែលល្អបំផុតចំពោះ validation data។ រូបខាងក្រោមបង្ហាញពីការប្រៀបធៀបចំពោះតម្លៃមួយចំនួននៃ$\ \alpha\ $ ។

markers = ['-','-','-.','-.']
alphas = [1e-9,1e-3,1e-2,1]
w_fit = []
d = 9
plt.scatter(Xtrain,Ytrain,marker='o',color='black')
plt.scatter(Xtest,Ytest,marker='o',color='red')
for i,alpha in enumerate(alphas):
  w = ridge_fit(Xtrain,Ytrain,d,alpha)
  #w = ridge_sgd_fit(Xtrain,Ytrain,d,alpha)
  w_fit.append(w)
  xa = np.linspace(min(Xtrain)-0.1,max(Xtrain)+0.1,100)
  ya = predict(xa,w,d)
  plt.plot(xa,ya,markers[i])
plt.grid()
plt.plot(xa,predict(xa,fit(Xtrain,Ytrain,d),d),'g-.')
plt.ylim([-1.6,1.6])
plt.legend(['alpha='+str(i) for i in alphas]+['no regulization','training data','test data'])
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Linear Regression Model (Polynomial degree=9)')
plt.show()