ម៉ូឌែលតម្រែតម្រង់លីនេអ៊ែរ(២)¶

ការសិក្សាលើទំនាក់ទំនងរវាងច្រើនអថេរ¶

ក្នុងការសិក្សាលើទំនាក់ទំនងរវាងអថេរច្រើន ចំនួនអថេរពន្យល់អាចមានលើសពីមួយ។ ជាឧទាហរណ៍ បើក្នុងករណីក្នុងមេរៀនមុន អថេរពន្យល់អាចមានអថេរក្រៅពីកម្ពស់ដូចជាអាយុ ទំហំចង្កេះ ឬអថេរផ្សេងៗទៀត។

ក្នុងករណីអថេរពន្យល់ច្រើនបែប នេះយើងសន្មតម៉ូឌែលដូចខាងក្រោម។

\[y=f(x)=\beta_0+\beta_1 x_1+\beta_2 x_2+\ldots+\beta_d x_d\]

ទោះបីជាចំនួននៃអថេរពន្យល់មានការកើនឡើងក្តី ការវិភាគដោយប្រើម៉ូឌែលតម្រែតម្រង់លីនេអ៊ែរមិនមានអ្វីប្រែប្រួលជាធំដុំនោះឡើយ។ អ្នកអាចបង្ហាញម៉ូឌែលខាងលើជាទម្រង់វ៉ិចទ័រនិងម៉ាទ្រីសរួចសិក្សាដូចគ្នា។

\[\begin{split} X=\left(\begin{matrix}\begin{matrix}1&x_{11}&\cdots\\\vdots&\vdots&\cdots\\1&x_{N1}&\cdots\\\end{matrix}&\begin{matrix}x_{1d}\\\vdots\\x_{Nd}\\\end{matrix}\\\end{matrix}\right)\in\mathbb{R}^{N\times\left(d+1\right)}\ ,\ \pmb{y}=\left(\begin{matrix}y_1\\\vdots\\y_N\\\end{matrix}\right)\in\mathbb{R}^N\ ,\ \pmb{\epsilon}=\left(\begin{matrix}\epsilon_1\\\vdots\\\epsilon_N\\\end{matrix}\right)\in\mathbb{R}^N\ ,\ \pmb{\beta}=\left(\begin{matrix}\beta_0\\\vdots\\\beta_d\\\end{matrix}\right)\in\mathbb{R}^{d+1} \end{split}\]

ពេលនេះម៉ូឌែលនិងផលបូកតម្លៃការេនៃលម្អៀងខាងលើអាចសរសេរដូចខាងក្រោម។

\[ \pmb{y}=X\pmb{\beta}+\pmb{\epsilon} \]

\[ E\left(\pmb{\beta}\right)=\sum_{i=1}^{N}\epsilon_i^2=\left(\pmb{y}-X\pmb{\beta}\right)^\top\left(\pmb{y}-X\pmb{\beta}\right) \]

ដោយប្រើវិធីសាស្រ្តLeast Square Error ដូចក្នុងមេរៀនមុនយើងបានលទ្ធផលដូចគ្នា។

\[ \hat{\pmb{\beta}}=\left(X^\top X\right)^{-1}X^T\pmb{y} \]

ក្នុងករណីខ្លះការប្រើប្រាស់តម្លៃផ្ទាល់នៃអថេរពន្យល់មិនអាចពណ៌នាទំនាក់ទំនងរវាងអថេរគោលដៅនិងអថេរពន្យល់បានល្អឡើយដូចក្នុងករណីរូបខាងក្រោម។

import numpy as np 
import matplotlib.pyplot as plt

X = np.array([ 0.  ,  0.11,  0.25,  0.29,  0.41,  0.42,  0.43,  0.8 ,  0.81, 1.  ])
Y = np.array([ 0.04,  0.75,  1.  ,  0.99,  0.31,  0.52,  0.38, -0.99, -1.05, 0.  ])
xa = np.linspace(min(X),max(X),1000)
plt.scatter(X,Y,color='b',label='observed-data')
plt.xlabel("x")
plt.ylabel("y")
plt.grid()
plt.legend()
plt.title("Figure1")

plt.show()

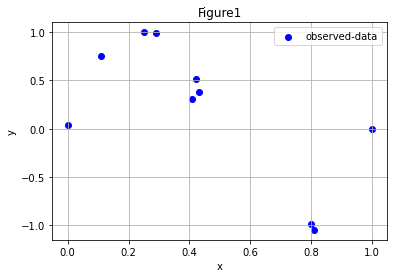
ហេតុនេះការបម្លែងតម្លៃអថេរពន្យល់ត្រូវបានអនុវត្ត។ ជាឧទាហរណ៍ដូចជាការប្រើអនុគមន៍ដឺក្រេទី២ ឬខ្ពស់ជាងនេះ ឬការប្រើអនុគមន៍មិនមែនលីនេអ៊ែរជាដើម។ ក្នុងករណីនេះម៉ូឌែលតម្រែតម្រង់លីនេអ៊ែរអាចបង្ហាញដូចខាងក្រោម។នៅទីនេះទោះបីជាអនុគមន៍ \(\phi_i\left(x\right)\) ជាទម្រង់មិនលីនេអ៊ែរក្តី ការហៅថាម៉ូឌែលតម្រែតម្រង់លីនេអ៊ែរ ព្រោះចង់សង្កត់ធ្ងន់លើផលបូកជាទម្រង់លីនេអ៊ែរនៃអនុគមន៍ទាំងអស់នោះ។

\[ y=f\left(x\right)=\beta_0\phi_0\left(x\right)+\beta_1\phi_1\left(x\right)+\ldots+\beta_d\phi_d\left(x\right) \]

ករណីប្រើពហុធាដឺក្រេទី៣យើងបាន

\[ y=\beta_0+\beta_1x+\beta_2x^2+\beta_3x^3 \]

អ្នកអាចបង្ហាញម៉ូឌែលខាងលើជាទម្រង់វ៉ិចទ័រនិងម៉ាទ្រីសរួចសិក្សាដូចគ្នា។

\[\begin{split} X=\left(\begin{matrix}\begin{matrix}1&x_1&x_1^2\\\vdots&\vdots&\cdots\\1&x_N&x_N^2\\\end{matrix}&\begin{matrix}x_1^3\\\vdots\\x_N^3\\\end{matrix}\\\end{matrix}\right)\in\mathbb{R}^{N\times4}\ ,\ \pmb{y}=\left(\begin{matrix}y_1\\\vdots\\y_N\\\end{matrix}\right)\in\mathbb{R}^N\ ,\ \pmb{\epsilon}=\left(\begin{matrix}\epsilon_1\\\vdots\\\epsilon_N\\\end{matrix}\right)\in\mathbb{R}^N\ ,\ \pmb{\beta}=\left(\begin{matrix}\beta_0\\\vdots\\\beta_3\\\end{matrix}\right)\in\mathbb{R}^4\ \end{split}\]

def fit(x,y,k):
  X_ = np.zeros((len(x),k+1))
  for i in range(k+1):
    X_[:,i] = x**i
  w = np.linalg.inv(X_.T@X_)@X_.T@y
  return w

def predict(x,w,k):
  X_ = np.zeros((len(x),k+1))
  for i in range(k+1):
    X_[:,i] = x**i
  return X_@w

w = fit(X,Y,3)
print(w)

cov_YY = np.cov(predict(X,w,3),Y)
R2 = cov_YY[0,0]/cov_YY[1,1]
print("R2=%.3f"%(R2))
xa = np.linspace(min(X),max(X),1000)
ya = predict(xa,w,3)
plt.scatter(X,Y,color='b')
plt.plot(xa,ya,'r-')
plt.xlabel("x")
plt.ylabel("y")
plt.grid()
y_legend = "y="+str(round(w[0],3))+"+"+str(round(w[1],3))+"x"+str(round(w[2],3))+"x^2"
plt.legend([y_legend,"observed-data"])
plt.title("Figure2")

plt.show()

[ 1.14996701e-02  1.05535056e+01 -3.17324025e+01  2.11628099e+01]
R2=0.990

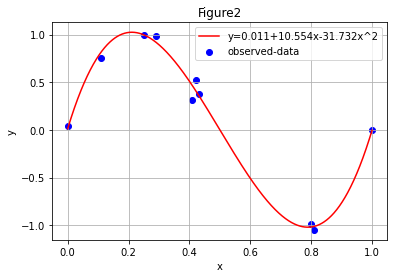
បើយើងជ្រើសយកម៉ូឌែលជាទម្រង់ពហុធាដឺក្រេទី៩ នោះយើងនឹងបានលទ្ធផលដូចខាងក្រោម។

X = np.array([ 0.  ,  0.11,  0.25,  0.29,  0.41,  0.42,  0.43,  0.8 ,  0.81, 1.  ])
Y = np.array([ 0.04,  0.75,  1.  ,  0.99,  0.31,  0.52,  0.38, -0.99, -1.05, 0.  ])
w = fit(X,Y,9)
print("w=",w)
xa = np.linspace(min(X),max(X),1000)
ya = predict(xa,w,9)
plt.scatter(X,Y,color='b')
plt.plot(xa,ya,'r-')
plt.xlabel("x")
plt.ylabel("y")
plt.grid()
plt.legend(["model","observed-data"])
plt.title("Figure3")
plt.show()

w= [ 4.87395932e-02  1.98384029e+02 -4.47755792e+03  4.08986697e+04
 -1.95961522e+05  5.43625437e+05 -9.03237557e+05  8.85913047e+05
 -4.72733950e+05  1.05775053e+05]

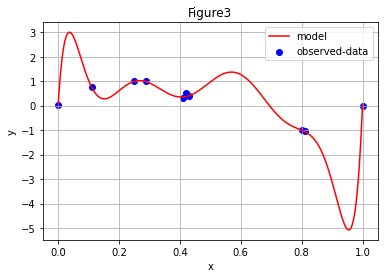
តាមការសង្កេត អ្នកអាចនឹងមើលឃើញថាប្រសិនបើយើងតម្លើងដឺក្រេនៃពហុធានោះកម្រិតនៃការពណ៌នារបស់ម៉ូឌែលលើទិន្នន័យនឹងមានការកើនឡើង។ ប៉ុន្តែការបង្ហាញម៉ូឌែលដែលមានភាពស្មុគស្មាញពេកអាចត្រឹមតែពណ៌នាលើទិន្នន័យដែលមានតែប៉ុណ្ណោះ ផ្ទុយទៅវិញវាមិនអាចទស្សន៍ទាយបានល្អឡើយចំពោះទិន្នន័យដែលមិនមានក្នុងដៃ។រូបភាពទី៥បង្ហាញករណីនេះ។

ក្នុងរូបទី3នេះ បើយើងគណនា Coefficient of determination (\(\pmb{R}^\mathbf{2}\))យើងនឹងបានតម្លៃ \(1\) ដែលជាតម្លៃយ៉ាងល្អក្នុងការពណ៌នាទិន្នន័យដែលមានក្នុងដៃ។ ប៉ុន្តែបើយើងសង្កេតលើគម្រូទិន្នន័យជាក់ស្តែង និងក្រាបនៃម៉ូឌែល តម្លៃនៃការទស្សន៍ទាយត្រង់តំបន់ដែលគ្មានទិន្នន័យ គឺគ្មានលំនឹង និងចេញផុតឆ្ងាយពីដែននៃទិន្នន័យដែលមានក្នុងដៃ។

ហេតុនេះក្នុងការជ្រើសរើសម៉ូឌែល អ្នកគួរសង្កេតលើចរិតលក្ខណៈនៃទិន្នន័យព្រមទាំងភាពល្អប្រសើរនៃការពន្យល់របស់វាចំពោះទាំងទិន្នន័យដែលមានក្នុងដៃស្រាប់ និងទិន្នន័យដែលមិនមានពោលគឺភាពប្រសើរក្នុងការទស្សន៍ទាយឬប៉ាន់ស្មាននាពេលអនាគត។

Machine Learning

ម៉ូឌែលតម្រែតម្រង់លីនេអ៊ែរ(២)¶

ការសិក្សាលើទំនាក់ទំនងរវាងច្រើនអថេរ¶