Feedforward Neural Network¶

ក្នុងអត្ថបទមុន យើងបានសិក្សាអំពីPerceptron ដែលជាម៉ូឌែលអាចបែងចែកទិន្នន័យបំណែងចែកលីនេអ៊ែរបានយ៉ាងងាយដោយការកំណត់តម្លៃប៉ារ៉ាម៉ែត្រសមស្រប។ លើសពីនេះ ក្នុងករណីទិន្នន័យមិនអាចបែងចែកលីនេអ៊ែរ ការបង្កើនចំនួនថ្នាក់នៃPerceptronត្រូវបានប្រើប្រាស់។ ម៉ូឌែលបែបនេះហៅថា Multilayer Perceptron។ ដោយការភ្ជាប់ណឺរ៉ូន (node) ច្រើនបន្តគ្នាជាច្រើនថ្នាក់ដែលស្រដៀងគ្នានឹងទម្រង់នៃប្រព័ន្ធប្រសាទរបស់ភាវៈរស់ផងនោះម៉ូឌែលបែបនេះក៏ត្រូវបានគេហៅថា Aritificial Neural Network ផងដែរ។

លទ្ធផលបញ្ជូនបន្តនៃណឺរ៉ូន¶

Feedforward Neural Network (FNN) គឺជាទម្រង់មួយនៃArtificial Neural Network ដែលមានណឺរ៉ូន(node)ច្រើនតម្រៀបគ្នាជាថ្នាក់និងភ្ជាប់គ្នានិងគ្នារវាងថ្នាក់នៅជាប់បន្តបន្ទាប់គ្នាដោយទម្ងន់ផ្ទាល់ខ្លួន។ សញ្ញាណឬធាតុចូលនៃFNNត្រូវបានបញ្ជូនពីផ្នែកថ្នាក់ធាតុចូល(input layer) ទៅកាន់ផ្នែកនៃថ្នាក់លទ្ធផល(output layer)តាមទិសតែមួយ។ លទ្ធផលដែលបញ្ចេញដោយណឺរ៉ូននៅថ្នាក់លទ្ធផលត្រូវបានគណនាដូចក្នុងករណីPerceptronទម្រង់ធម្មតាដែរ ប៉ុន្តែនៅទីនេះលទ្ធផលមិនគ្រាន់តែប្រៀបធៀបផលបូកនៃធាតុចូលនិងកម្រិតកំណត់(threshold)នៃណឺរ៉ូនប៉ុណ្ណោះទេ តែអនុគមន៍មិនលីនេអ៊ែរត្រូវបានអនុវត្តលើលទ្ធផលនៃផលបូកនោះដើម្បីកំណត់នូវលទ្ធផលដែលត្រូវបញ្ជូនបន្ត។ អនុគមន៍ដែលអនុវត្តលើលទ្ធផលនៃផលបូកធាតុចូលនេះហៅថា អនុគមន៍សកម្ម(activation function)។ យើងនឹងធ្វើការបកស្រាយលម្អិតអំពីអនុគមន៍សកម្មនៅចំណុចបន្ទាប់។

នៅពេលដែលធាតុចូល $x_1,x_2,\ldots,x_d$ ត្រូវបានបញ្ជូនមកកាន់ណឺរ៉ូន(រូបទី១) ដែលមានទម្ងន់ផ្ទាល់នៃធាតុចូលរៀងគ្នា $w_1,w_2,\ldots,w_d$ នោះ ផលបូកនៃធាតុចូលសរុបកំណត់ដោយ $u$ និងលទ្ធផលបញ្ជូនបន្តនៃណឺរ៉ូននោះត្រូវបានកំណត់ដោយ $z$ ដូចទម្រង់ខាងក្រោម។ នៅទីនេះ $b$ ហៅថា bias ។

\[ u=w_1x_1+w_2x_2+\ldots+w_dx_d+b \]

\[ z=f\left(u\right)=\ f\left(w_1x_1+w_2x_2+\ldots+w_dx_d+b\right) \]

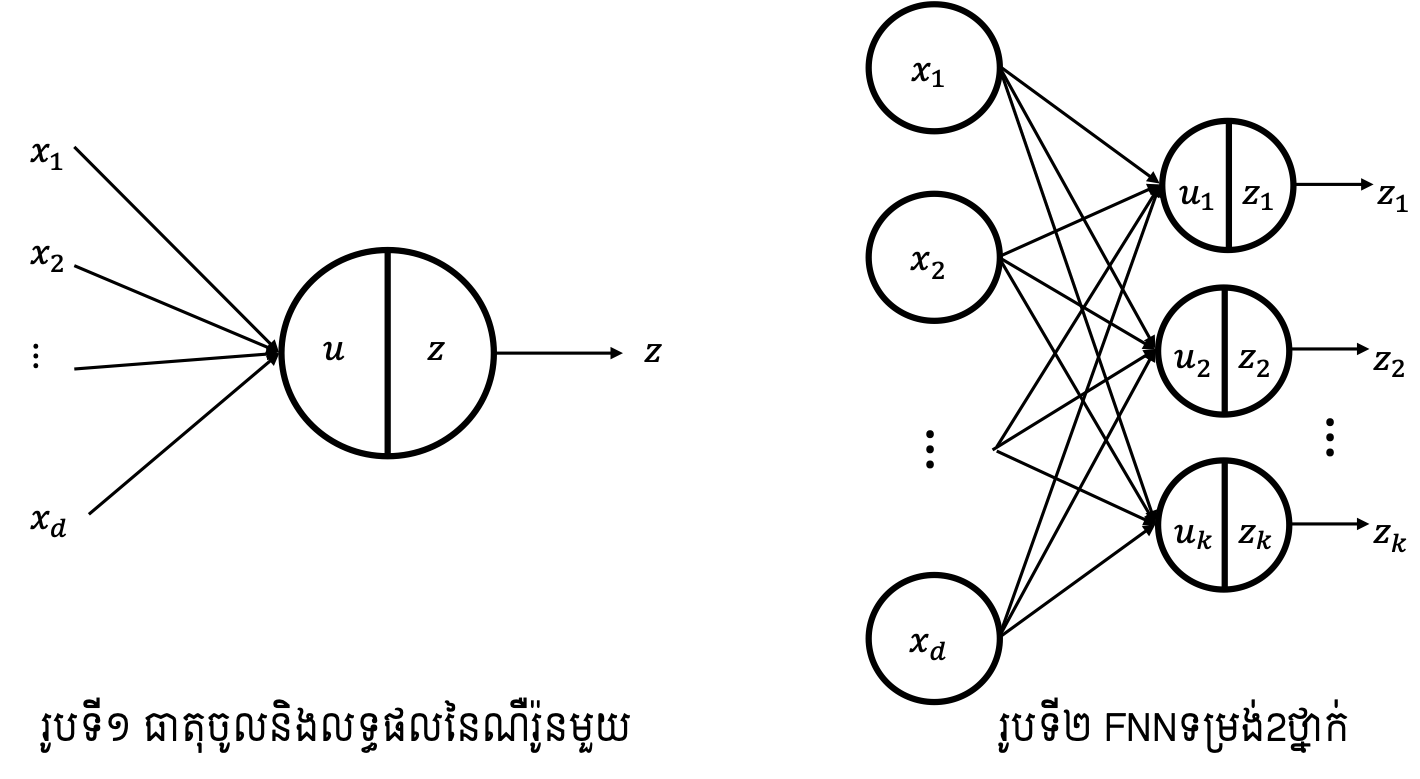
FNN-model

ក្នុងករណីទម្រង់2ថ្នាក់ដូចក្នុងរូបទី២ សញ្ញាណត្រូវបានបញ្ជូនបន្តបន្ទាប់។ សន្មតថានៅថ្នាក់ទី១មានណឺរ៉ូនចំនួន $d$ និង នៅថ្នាក់ទី២មានណឺរ៉ូនចំនួន $k$ នោះលទ្ធផលបញ្ជូនបន្តនៃណឺរ៉ុននៅថ្នាក់លទ្ធផលទី២ត្រូវបានបង្ហាញក្នុងទម្រង់ខាងក្រោម

\[ \left(i=1,2,\ldots,k\right) \]

។

\[ u_i=\sum_{j=1}^{d}{w_{ij}x_j}+b_i \]

\[ z_i=f\left(u_i\right) \]

យើងក៏អាចបង្ហាញជាទម្រង់វ៉ិចទ័រនិងម៉ាទ្រីសដូចខាងក្រោមផងដែរ។

\[ \pmb{u}=\pmb{Wx}+\pmb{b} \]

\[ \pmb{z}=\pmb{f}\left(\pmb{u}\right) \]

\[ \begin{align}\begin{aligned}\begin{split} \pmb{u}=\left[\begin{matrix}u_1\\\vdots\\u_k\\\end{matrix}\right]\ ,\ \pmb{x}=\left[\begin{matrix}x_1\\\vdots\\x_d\\\end{matrix}\right]\ ,\ \pmb{b}=\left[\begin{matrix}b_1\\\vdots\\b_k\\\end{matrix}\right]\ ,\ \pmb{z}=\left[\begin{matrix}z_1\\\vdots\\z_k\\\end{matrix}\right]\ ,\ \pmb{f}\left(\pmb{u}\right)=\left[\begin{matrix}f{(u}_1)\\\vdots\\f(u_k)\\\end{matrix}\right]\end{split}\\\begin{split} \pmb{W}=\left[\begin{matrix}w_{11}&\cdots&w_{1d}\\\vdots&\ddots&\vdots\\w_{k1}&\cdots&w_{kd}\\\end{matrix}\right] \end{split}\end{aligned}\end{align} \]

អនុគមន៍សកម្ម Activation Function¶

import numpy as np
import matplotlib.pyplot as plt

អនុគមន៍សកម្ម(activation function) គឺជាអនុគមន៍ដែលគ្រប់គ្រងលើកម្រិតនៃការបញ្ជូនបន្តនូវលទ្ធផលរបស់ណឺរ៉ូននិមួយៗ។ ជាទូទៅអនុគមន៍សកម្មមានទម្រង់ជាអនុគមន៍មិនលីនេអ៊ែរកើនដាច់ខាត។ មានទម្រង់ជាច្រើនត្រូវបានប្រើជាអនុគមន៍សកម្មដូចជា អនុគមន៍Sigmoid,អនុគមន៍Tanh,អនុគមន៍Softmax,អនុគមន៍ReLU(rectified linear function)ជាដើម។

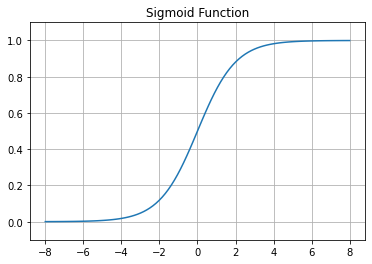
អនុគមន៍Sigmoid $\sigma\left(\bullet\right)$ មានដែនកំណត់លើសំណុំចំនួនពិត$\left(-\infty,\infty\right)$និងយកសំណុំរូបភាពលើចន្លោះបើក$\left(0,1\right)$។ អនុគមន៍បែបនេះអាចផ្តល់នូវលទ្ធផលដែលយើងអាចបកស្រាយបានជាតម្លៃប្រូបាបនៃការបញ្ជូនបន្តឬមិនបញ្ជូនបន្ត$(1/0)$។

\[ f\left(u\right)=\sigma\left(u\right)=\frac{1}{1+e^{-u}} \]

def sigmoid(x):
  return 1/(1+np.exp(-x))

x = np.linspace(-8,8,100)
plt.plot(x,sigmoid(x),label='sigmoid')
plt.grid()
plt.ylim([-0.1,1.1])
plt.title("Sigmoid Function")
plt.show()

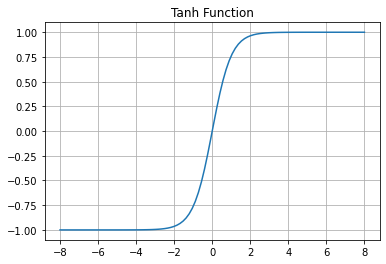
អនុគមន៍Tanh $\tanh{\left(\bullet\right)}$ មានដែនកំណត់លើសំណុំចំនួនពិត$\left(-\infty,\infty\right)$ និងយកសំណុំរូបភាពលើចន្លោះបើក$\left(-1,1\right)$។ អនុគមន៍បែបនេះមានលក្ខណៈស្រដៀងនឹងអនុគមន៍Sigmoidដែរ ដែលអាចផ្តល់នូវលទ្ធផលដែលមានបម្រែបម្រួលតិចតួចក្បែរតម្លៃថេរនៅពេលដែលតម្លៃនៃធាតុចូលធំខ្លាំងដល់កម្រិតណាមួយ និងប្រែប្រួលខ្លាំងនៅពេលដែលធាតុចូលមានតម្លៃក្បែរ0។

\[ f\left(u\right)=\tanh{\left(u\right)}=\frac{e^u-e^{-u}}{e^u+e^{-u}} \]

def tanh(x):
  return (np.exp(x)-np.exp(-x))/(np.exp(x)+np.exp(-x))

x = np.linspace(-8,8,100)
plt.plot(x,tanh(x),label='tanh')
plt.grid()
plt.ylim([-1.1,1.1])
plt.title("Tanh Function")
plt.show()

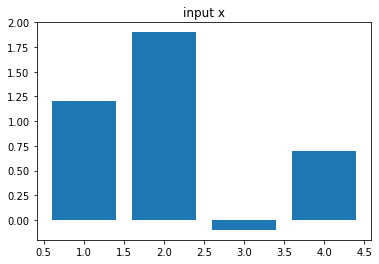
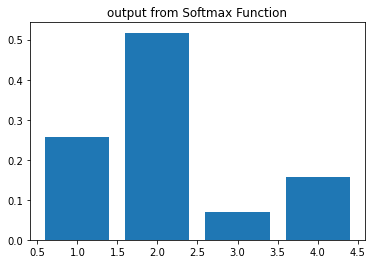
អនុគមន៍Softmax $softmax\left(\bullet\right)$ មានដែនកំណត់លើវ៉ិចទ័រចំនួនពិត$\mathbb{R}^d $និងយកសំណុំរូបភាពលើចន្លោះបើក$\left(0,1\right)^d$ដែលមានផលបូកគ្រប់កំប៉ូសង់ស្មើ 1។ អនុគមន៍បែបនេះអាចផ្តល់នូវលទ្ធផលដែលយើងអាចបកស្រាយបានជាតម្លៃប្រូបាបនៃលទ្ធផលដែលអាចចេញជាdប្រភេទផ្សេងៗគ្នាបាន។ក្នុងករណីd=2 អនុគមន៍នេះសមមូលនឹងអនុគមន៍Sigmoid។ចំពោះ $\pmb{u}=\left(\begin{matrix}u_1&\cdots&u_d\\\end{matrix}\right)^\top$

\[ f\left(\pmb{u}\right)=Softmax{\left(\pmb{u}\right)}=(Softmax(u_1)　\cdots　Softmax(u_d))^\top \]

\[ Softmax\left(u_i\right)=\frac{e^{u_i}}{\sum_{j=1}^{d}e^{u_j}} \]

def softmax(x):
  exp_x = np.exp(x - np.max(x))
  return exp_x/np.sum(exp_x)

a = np.array([1,2,3,4])
x = np.array([1.2, 1.9, -0.1, 0.7])
y = softmax(x)
plt.bar(a,x)
plt.title("input x")
plt.show()
plt.bar(a,y)
plt.title("output from Softmax Function")
plt.show()

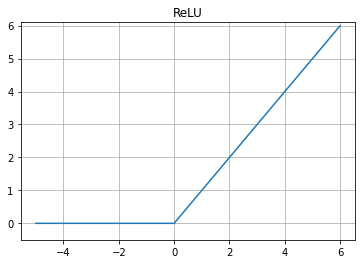
អនុគមន៍rectifier $linear: ReLU{\left(\bullet\right)}$ មានដែនកំណត់លើសំណុំចំនួនពិត$\left(-\infty,\infty\right)$ និងយកសំណុំរូបភាពលើចន្លោះបើក$\left(0,\infty\right)$។ នៅពេលដែលធាតុចូលមានតម្លៃតូចជាងឬស្មើសូន្យ លទ្ធផលបញ្ជូនបន្តត្រូវបានកំណត់ដោយ 0 និងបញ្ជូនបន្តនូវតម្លៃដូចធាតុចូលដដែលបើធាតុចូលមានតម្លៃធំជាងឬស្មើសូន្យ។អនុគមន៍បែបនេះមានលក្ខណៈស្រដៀងនឹងអនុគមន៍ដឺក្រេទី១(លីនេអ៊ែរ)ដែរ ដែលអាចប្រើក្នុងករណីប៉ាន់ស្មានទាំងម៉ូឌែលលីនេអ៊ែរនិងមិនលីនេអ៊ែរបានល្អ។

\[ f\left(u\right)=ReLU\left(u\right)=\max{\left(u,0\right)} \]

def ReLU(x):
  return np.maximum(0,x)

x = np.linspace(-5,6,100)
plt.plot(x,ReLU(x),label='ReLU')
plt.grid()
plt.ylim([-0.5,6.1])
plt.title("ReLU")
plt.show()

បណ្តាញច្រើនថ្នាក់ (Multilayer Network)¶

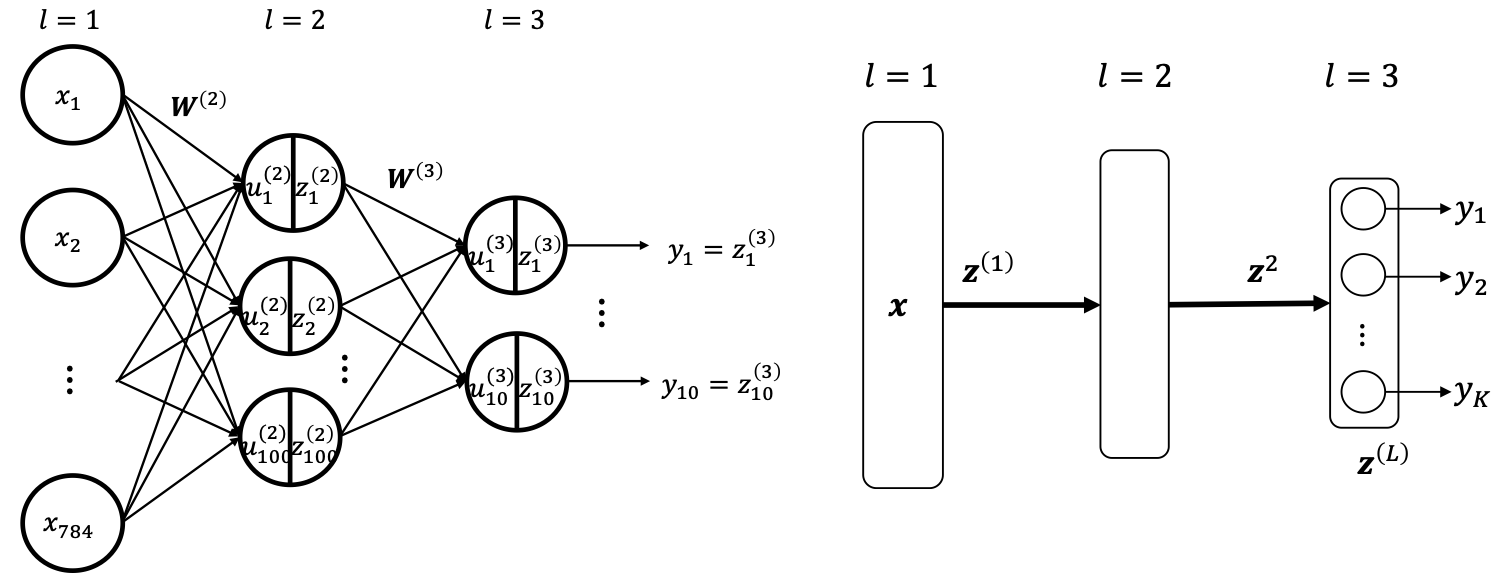
នៅចំណុចនេះយើងពិនិត្យលើករណីម៉ូឌែលដែលមានច្រើនថ្នាក់ដូចក្នុងរូបទី៥។ ព័ត៌មាន (សញ្ញាណឬធាតុចូល)ត្រូវបានបញ្ជូនតាមលំដាប់លំដោយពីថ្នាក់នៅខាងឆ្វេងទៅស្តាំ។ នៅទីនេះយើងកំណត់ហៅថ្នាក់និមួយៗដោយ$l=1,2,3,\ldots$។ ក្នុងរូបខាងលើថ្នាក់ $l=1$ពោលគឺថ្នាក់នៅខាងឆ្វេងបំផុតហៅថាថ្នាក់នៃធាតុចូល(input layer), ថ្នាក់$l=2$ ហៅថាថ្នាក់នៃធាតុកណ្តាល(internal layer, hidden layer), ថ្នាក់l=3 ពោលគឺថ្នាក់នៅខាងស្តាំបំផុត ហៅថាថ្នាក់នៃលទ្ធផល(output layer) ។ លទ្ធផលនៅថ្នាក់និមួយៗអាចសរសេរជាទម្រង់ដូចខាងក្រោម។

\[ \pmb{u}^{\left(2\right)}=\pmb{W}^{\left(2\right)}\pmb{x}+\pmb{b}^{\left(2\right)}\ \ \ \ \ \ \ \ ,\ \ \pmb{z}^{\left(2\right)}=\pmb{f}\left(\pmb{u}^{\left(2\right)}\right) \]

\[ \pmb{u}^{\left(3\right)}=\pmb{W}^{\left(3\right)}\pmb{z}^{\left(2\right)}+\pmb{b}^{\left(3\right)}\ \ \ \ \ \ \ \ ,\ \ \pmb{z}^{\left(3\right)}=\pmb{f}\left(\pmb{u}^{\left(3\right)}\right) \]

ជាទូទៅ លទ្ធផលនៅថ្នាក់កណ្តាលកំណត់ដោយ

\[ \pmb{u}^{\left(l+1\right)}=\pmb{W}^{\left(l+1\right)}\pmb{z}^{\left(l\right)}+\pmb{b}^{\left(l+1\right)}\ \ \ \ \ \ \ \ ,\ \ \pmb{z}^{\left(l+1\right)}=\pmb{f}\left(\pmb{u}^{\left(l+1\right)}\right) \]

និង លទ្ធផលនៅថ្នាក់លទ្ធផលចុងក្រោយកំណត់ដោយ

\[ \pmb{y}\equiv\pmb{z}^{\left(l+1\right)} \]

FNN-Multilayer Network

ដូចដែលបានឃើញក្នុងទម្រង់គណនាខាងលើ ក្នុងFNN សញ្ញាណត្រូវបានបញ្ជូនបន្តបន្ទាប់ដោយការគណនាក្នុងរបៀបដូចគ្នាពីមួយថ្នាក់ទៅមួយថ្នាក់។ នេះគឺជាប្រភពដែលម៉ូឌែលនេះត្រូវបានហៅថា feedforward ។ ទម្ងន់ផ្ទាល់នៃណឺរ៉ូនចំពោះធាតុចូលតាមថ្នាក់និមួយៗ$\pmb{W}^{\left(l\right)}$ និង bias $\pmb{b}^{\left(l\right)}$ត្រូវបានហៅជារួមថាជា ប៉ារ៉ាម៉ែត្រនៃបណ្តាញ។ ក្នុងអត្ថបទនេះនិងបន្តបន្ទាប់យើងកំណត់ហៅដោយងាយនូវ បណ្តាញដែលមានប៉ារ៉ាម៉ែត្រ(ហៅជារួម)$\pmb{w}$ និងធាតុចូល $\pmb{x}$ ដោយ $\pmb{y}\left(\pmb{x};\pmb{w}\right)$។

ការកំណត់ទម្រង់ណឺរ៉ូននៅថ្នាក់លទ្ធផលនិងអនុគមន៍លម្អៀង¶

ប្រភេទនៃបញ្ហានិងវិធីសាស្រ្តរៀន(Learning)¶

ដូចដែលបានរៀបរាប់ពីអត្ថបទមុននិងចំណុចខាងលើ បណ្តាញដែលបង្ហាញដោយទម្រង់ នៃអនុគមន៍ច្រើនអថេរ$\pmb{y}\left(\pmb{x};\pmb{w}\right)$នឹងប្រែប្រួលនៅពេលដែលប៉ារ៉ាម៉ែត្ររបស់វាត្រូវបានផ្លាស់ប្តូរ។ ការជ្រើសរើសប៉ារ៉ាម៉ែត្របានល្អ នឹងធ្វើឱ្យបណ្តាញ(network)អាចបង្ហាញនូវអនុគមន៍ឬបញ្ហាដែលមានបានល្អប្រសើរ។

សន្មតថា អនុគមន៍ឬបញ្ហាជាគោលដៅដែលយើងចង់បង្ហាញដោយNeural Network មិនប្រែប្រួលសណ្ឋានខាងក្នុងរបស់វាឡើយ ហើយទទួលធាតុចូល $\pmb{x}$ និងបញ្ជូនចេញនូវលទ្ធផល $\pmb{t}$ ។ គូនៃទិន្នន័យបែបនេះជាច្រើនត្រូវបានផ្តល់ឱ្យ $\left\{\left(\pmb{x}_1,\pmb{t}_1\right),\ldots,\left(\pmb{x}_N,\pmb{t}_N\right)\right\}$ ។ នៅក្នុងអត្ថបទនេះ និងអត្ថបទបន្តបន្ទាប់ គូនិមួយៗហៅថាជាគម្រូសម្រាប់រៀន(training sample) ហើយសំណុំទាំងមូលហៅថា សំណុំទិន្នន័យសម្រាប់រៀន(training data)។

ដោយធ្វើការកែសម្រួលនិងកំណត់នូវតម្លៃប៉ារ៉ាម៉ែត្រ យើងអាចធ្វើការបង្ហាញទំនាក់ទំនងដែលមានក្នុងទិន្នន័យឡើងវិញបានដោយបណ្តាញ(network)របស់យើង។ ពោលគឺចំពោះគម្រូសម្រាប់រៀន$\left(\pmb{x}_n,\pmb{t}_n\right)$និមួយៗ យើងចង់កំណត់នូវប៉ារ៉ាម៉ែត្រណាដែលធ្វើឱ្យយើងអាចទទួលបាន $\pmb{y}\left(\pmb{x}_n;\pmb{w}\right)$ ដែលមានតម្លៃជិតបំផុតនៅនឹង$\pmb{t}_n$។ ដំណើរកំណត់រកនូវប៉ារ៉ាម៉ែត្រដោយប្រើសំណុំទិន្នន័យសម្រាប់រៀនបែបនេះសន្មតហៅថាជាដំណើរការរៀន(learning process)។

ហេតុនេះការប្រៀបធៀបរវាងតម្លៃលទ្ធផល$\pmb{y}\left(\pmb{x}_n;\pmb{w}\right)$ ដែលផ្តល់ដោយបណ្តាញនិងតម្លៃ$\pmb{t}_n$ត្រូវបានធ្វើឡើង។ ដើម្បីបង្ហាញពីកម្រិតជិតគ្នានៃតម្លៃទាំងពីរយើងកំណត់រង្វាស់សម្រាប់វាស់កម្រិតនេះ។ រង្វាស់នេះយើងសន្មតហៅថាជា អនុគមន៍កម្រិតលម្អៀង(error function,loss function)។ ការកំណត់ប្រភេទនៃអនុគមន៍កម្រិតលម្អៀងខុសគ្នាទៅតាមប្រភេទចំណោទបញ្ហាដែលយើងចង់ដោះស្រាយ។

ចំណោទតម្រែតម្រង់¶

ចំណោទតម្រែតម្រង់(Regression) គឺជាប្រភេទចំណោទដែលធ្វើការកំណត់នូវអនុគមន៍ ដើម្បីបង្ហាញនូវទំនាក់ទំនងរវាងធាតុចូលនិងលទ្ធផលដែលមានទម្រង់ជាអថេរជាប់។ ហេតុនេះក្នុង ករណីនៃចំណោទតម្រែតម្រង់ យើងកំណត់យកអនុគមន៍សកម្ម(activation function)នៅថ្នាក់លទ្ធផលនៃបណ្តាញ(FNN)ដោយអនុគមន៍ដែលផ្តល់នូវសំណុំរូបភាពដូចដែននៃលទ្ធផលរបស់សំណុំទិន្នន័យសម្រាប់រៀន។ ឧទាហរណ៍ ក្នុងករណីដែលសំណុំទិន្នន័យសម្រាប់រៀនមានតម្លៃនៃលទ្ធផលលើចន្លោះ$[-1,1]$នោះយើងជ្រើសយកអនុគមន៍tanhសម្រាប់ជាអនុគមន៍សកម្ម។

ក្នុងករណីដែលសំណុំទិន្នន័យសម្រាប់រៀនមានតម្លៃនៃលទ្ធផលលើចន្លោះ$\left(-\infty,\infty\right)$នោះយើងជ្រើសយកអនុគមន៍ដែលផ្តល់តម្លៃដូចធាតុចូល Identity function សម្រាប់ជាអនុគមន៍សកម្ម។ ក្នុងករណីចំណោទតម្រែតម្រង់នេះដើម្បីប្រៀបធៀបកម្រិតជិតគ្នារវាងលទ្ធផលនៃបណ្តាញនិងតម្លៃលទ្ធផលនៃគម្រូសម្រាប់រៀន យើងប្រើផលបូកការេនៃតម្លៃលម្អៀង(sum of squared residuals) រវាងតម្លៃ$\pmb{y}\left(\pmb{x}_n;\pmb{w}\right)$ និង$\pmb{t}_n$ចំពោះគ្រប់គម្រូសម្រាប់រៀនក្នុងសំណុំទិន្នន័យសម្រាប់រៀនទាំងអស់។ ពោលគឺអនុគមន៍កម្រិតលម្អៀងសម្រាប់សំណុំទិន្នន័យសម្រាប់រៀនកំណត់ដោយ ។

\[ E\left(\pmb{w}\right)=\frac{1}{2}\sum_{i=1}^{N}{\left||\pmb{t}-\pmb{y}(\pmb{x_n},\pmb{w})|\right|^2} \]

នៅទីនេះការដាក់មេគុណ $\frac{1}{2}$ គឺដើម្បីសម្រួលដល់ការគណនាដល់ការធ្វើដេរីវេនាពេលខាងមុខ។

គោលដៅរបស់យើងគឺកំនត់ប៉ារ៉ាម៉ែត្រនៃបណ្តាញយ៉ាងណាដើម្បីឱ្យអនុគមន៍កម្រិតលម្អៀងខាងលើនេះមានតម្លៃអប្បបរមា។

ចំណោទធ្វើចំណាត់ថ្នាក់២ក្រុម¶

ក្នុងចំណោទធ្វើចំណាត់ថ្នាក់២ក្រុម ទិន្នន័យធាតុចូល $\pmb{x}$ នឹងត្រូវបែងចែកទៅក្នុងក្រុមមួយ ក្នុងចំណោមពីរក្រុម។ ឧទាហរណ៍ករណីធាតុចូលជារូបថតមួយសន្លឹក។ នៅពេលនោះក្រោយពីទាញយកលក្ខណៈសម្គាល់របស់រូបថតនោះជាទម្រង់វ៉ិចទ័ររួច បណ្តាញនឹងទទួលយកវ៉ិចទ័រនោះជាធាតុចូលរួចធ្វើការបែងចែកថាជារូបមុខមនុស្សឬមិនមែន។

ក្នុងករណីនេះ លទ្ធផលនៃទិន្នន័យសម្រាប់រៀន $t$ យកតម្លៃជាអថេរដាច់$\{1$(មុខមនុស្ស) , $0$(មិនមែនមុខមនុស្ស)$\}$។ បែបនេះចំណោទចំណាត់ថ្នាក់២ក្រុមក៏ជាចំណោទដែលទទួលធាតុចូល$\pmb{x}$ និងប៉ាន់ស្មានលទ្ធផល$t$ ដូចតម្រែតម្រង់ដែរគ្រាន់តែប្រភេទនៃតម្លៃលទ្ធផលជាអថេរដាច់។

ក្នុងករណីនេះ ដើម្បីប៉ាន់ស្មានតម្លៃលទ្ធផល យើងសិក្សាលើម៉ូឌែលប្រូបាប ពោលគឺសិក្សាលើប្រូបាបដែលថាលទ្ធផល$ t=1$នៅពេលធាតុចូល$ \pmb{x} $ត្រូវបានទទួល $p\left(t=1\middle|\pmb{x}\right) $។ គំនិតនៅទីនេះគឺថា បើប្រូបាបនេះមានតម្លៃធំជាង$0.5$ នោះយើងសន្និដ្ឋានថាលទ្ធផលគឺ$t=1$ និង សន្និដ្ឋានថាលទ្ធផលគឺ$ t=0 $ក្នុងករណីផ្ទុយពីនេះ។

ដោយពិនិត្យលើគំនិតបែបនេះ អ្នកអាចនឹកឃើញដល់លក្ខណៈនៃអនុគមន៍Sigmoid ដែលបានបង្ហាញខាងលើ។ បើយើងប្រើអនុគមន៍Sigmoid ជាអនុគមន៍សកម្មសម្រាប់បណ្តាញ FNN $\pmb{y}\left(\pmb{x};\pmb{w}\right)$ នោះយើងអាចបង្ហាញម៉ូឌែលប្រូបាបខាងលើដោយFNNបាន។

\[ p\left(t=1\middle|\pmb{x}\right)\approx\pmb{y}\left(\pmb{x};\pmb{w}\right) \]

ហេតុនេះដើម្បីកំណត់ប៉ារ៉ាម៉ែត្រនៃFNN យើងអាចសិក្សាពីសំណុំអថេរសម្រាប់រៀន(training data) $\left\{\left(\pmb{x}_n,t_n\right)\right\}_{n=1}^N$បានដោយកំណត់យកប៉ារ៉ាម៉ែត្រដែលធ្វើឱ្យបំណែងចែកប្រូបាប$ p\left(t\middle|\pmb{x};\pmb{w}\right)$ មានភាពប្រហាក់ប្រហែលគ្នាបំផុតជាមួយនឹងរបាយនៃសំណុំអថេរសម្រាប់រៀន។

ក្នុងការកំណត់ប៉ារ៉ាម៉ែត្រនៃម៉ូឌែលប្រូបាបបែបនេះ យើងហៅថា ការប៉ាន់ស្មានកម្រិតសាកសមបំផុតនៃទិន្នន័យ (Maximum Likelihood Estimation, MLE)។

ដោយប្រើតម្លៃនៃ$p\left(t=0\middle|\pmb{x};\pmb{w}\right),p\left(t=1\middle|\pmb{x};\pmb{w}\right) $យើងអាចបង្ហាញ $p\left(t\middle|\pmb{x};\pmb{w}\right)$ ជារួមតាមទម្រង់ខាងក្រោម។

\[ p\left(t\middle|\pmb{x};\pmb{w}\right)=p{\left(t=1\middle|\pmb{x};\pmb{w}\right)}^tp{\left(t=0\middle|\pmb{x};\pmb{w}\right)}^{1-t} \]

ដោយការសន្មតខាងលើ $p\left(t=1\middle|\pmb{x}\right)=y\left(\pmb{x};\pmb{w}\right)$ នោះ$p\left(t=1\middle|\pmb{x}\right)=1-y\left(\pmb{x};\pmb{w}\right)$ ។ ក្រោមការសន្មតនៃម៉ូឌែលបែបនេះ ការប៉ាន់ស្មានកម្រិតសាកសមបំផុតនៃទិន្នន័យ MLE គឺជាការកំណត់នូវកម្រិតសាកសមនៃទិន្នន័យ(likelihood)សម្រាប់រៀនរបស់ប៉ារ៉ាម៉ែត្រ$\pmb{w}$ និងជ្រើសយកតម្លៃនៃ$ \pmb{w} $ណាដែលធ្វើឱ្យកម្រិតសាកសមនោះមានតម្លៃអតិបរមា។ កម្រិតសាកសមនៃទិន្នន័យសម្រាប់រៀន(training data) របស់ប៉ារ៉ាម៉ែត្រ$\pmb{w}$ ត្រូវបានកំណត់ដូចទម្រង់ខាងក្រោម។

\[ L\left(\pmb{w}\right)=\prod_{n=1}^{N}{p\left(t_n\middle|\pmb{x};\pmb{w}\right)}=\prod_{n=1}^{N}{\left\{y\left(\pmb{x}_n;\pmb{w}\right)\right\}^{t_n}\left\{1-y\left(\pmb{x}_n;\pmb{w}\right)\right\}^{1-t_n}} \]

ដើម្បីសម្រួលដល់ការធ្វើបរមាកម្ម យើងអនុវត្តអនុគមន៍លោការីតលើកន្សោមខាងលើ។ការធ្វើបែបនេះមិនប៉ះពាល់ដល់អថេរភាព(ភាពកើនចុះ)នៃអនុគមន៍ឡើយ។ ក្នុងករណីនេះ អនុគមន៍កម្រិតលម្អៀងនៃចំណោទចំណាត់ថ្នាក់២ក្រុមកំណត់ដោយ $E\left(\pmb{w}\right)$ ដូចខាងក្រោម។

\[ E\left(\pmb{w}\right)=-\log{L\left(\pmb{w}\right)}=-\sum_{n=1}^{N}\left\{t_n\log{y\left(\pmb{x}_n;\pmb{w}\right)}+\left(1-t_n\right)\log{\left(1-y\left(\pmb{x}_n;\pmb{w}\right)\right)}\right\} \]

ដូចដែលបានបង្ហាញខាងលើ អនុគមន៍Sigmoidត្រូវបានប្រើសម្រាប់ជាអនុគមន៍សកម្មក្នុងថ្នាក់លទ្ធផលនៃFNN។ ចំណុចនេះអាចបកស្រាយដូចខាងក្រោម។

ប្រូបាប$ p\left(t=1\middle|\pmb{x}\right) $អាចសរសេរជាទម្រង់ប្រូបាបមានលក្ខខណ្ឌដូចខាងក្រោម។

\[ p\left(t=1\middle|\pmb{x}\right)=\frac{p\left(\pmb{x};t=1\right)}{p\left(\pmb{x};t=0\right)+p\left(\pmb{x};t=1\right)} \]

ដោយយក

\[ u\equiv\log{\frac{p\left(\pmb{x};t=1\right)}{p\left(\pmb{x};t=0\right)}} \]

នោះយើងបាន $$ p\left(t=1\middle|\pmb{x}\right)=\frac{1}{1+\exp{\left(-u\right)}}=\sigma\left(u\right) $$ ពោលគឺ ម៉ូឌែលប្រូបាប

\[ p\left(t=1\middle|\pmb{x}\right) \]

ដែលសិក្សាខាងលើសមមូលទៅនឹងអនុគមន៍Sigmoid។

ចំណោទធ្វើចំណាត់ថ្នាក់ច្រើនក្រុម¶

ក្នុងចំណោទធ្វើចំណាត់ថ្នាក់ច្រើនក្រុម ទិន្នន័យធាតុចូល$\pmb{x}$ នឹងត្រូវបែងចែកទៅក្នុងក្រុមមួយ ក្នុងចំណោមក្រុមមានកំណត់ច្រើន។ ឧទាហរណ៍ករណីធាតុចូលជារូបថតនៃលេខសរសេរដោយដៃមួយសន្លឹក។ នៅពេលនោះក្រោយពីទាញយកលក្ខណៈសម្គាល់របស់រូបថតនោះជាទម្រង់វ៉ិចទ័ររួចបណ្តាញនឹងទទួលយកវ៉ិចទ័រនោះជាធាតុចូលរួចធ្វើការបែងចែកថាជាលេខណាមួយក្នុងចំណោម 0 ដល់ 9។ ក្នុងករណីនេះ លទ្ធផលនៃទិន្នន័យសម្រាប់រៀន $t$ យកតម្លៃជាអថេរដាច់ $\{0,1, ... , 9\}$។

ក្នុងករណីនេះ ការប្រើបណ្តាញFNN សម្រាប់ចំណាត់ថ្នាក់ច្រើនក្រុម អាចធ្វើបានដោយកំណត់យកថ្នាក់លទ្ធផលមានចំនួនណឺរ៉ូនស្មើនឹងចំនួននៃក្រុមដែលត្រូវបែងចែក។ សន្មតថាចំនួនក្រុមដែលត្រូវបែងចែកក្នុងចំណោទមានK ។ នៅទីនេះ យើងប្រើបណ្តាញFNNដែលមានLថ្នាក់និងចំនួនណឺរ៉ូននៅថ្នាក់លទ្ធផលមានចំនួនK។ លទ្ធផលដែលផ្តល់ដោយណឺរ៉ូននិមួយៗក្នុងថ្នាក់លទ្ធផលអាចសរសេរដោយទម្រង់ខាងក្រោម។

\[ y_k\equiv z_k^{\left(L\right)}=\frac{\exp{\left(u_k^{\left(L\right)}\right)}}{\sum_{i=1}^{K}\exp{\left(u_i^{\left(L\right)}\right)}} \]

ដូចដែលបានបកស្រាយក្នុងចំណុចអនុគមន៍សកម្មខាងលើយើងអាចប្រើអនុគមន៍Sofmaxដើម្បីបម្លែងលទ្ធផលជាប្រូបាបនៃករណីបែងចែកចូលក្នុងក្រុមនិមួយៗ។ យើងនឹងពិនិត្យលើភាពត្រឹមត្រូវនៃការសន្មតនេះដោយប្រើម៉ូឌែលប្រូបាបដូចករណី២ក្រុមដែរ។

សន្មតថាថ្នាក់និមួយៗនៃចំណោទខាងលើគឺ $\mathcal{C}_1,\mathcal{C}_2,\ldots,\mathcal{C}_K $លទ្ធផលនៃណឺរ៉ូនkនៅថ្នាក់លទ្ធផលចុងក្រោយនៃបណ្តាញFNN កំណត់ដោយ $y_k\left(=z_k^{\left(L\right)}\right) $ជាប្រូបាបនៃព្រឹត្តិការណ៍ដែលធាតុចូល $\pmb{x}$ ត្រូវកំណត់ថានៅក្នុងក្រុម$\mathcal{C}_k$ ។

\[ p\left(\mathcal{C}_k|\pmb{x}\right)=y_k=z_k^{\left(L\right)} \]

ជាលទ្ធផល ធាតុចូល $\pmb{x}$ ត្រូវកំណត់ថានៅក្នុងក្រុម$\mathcal{C}_k$បើតម្លៃប្រូបាប$p\left(\mathcal{C}_k|\pmb{x}\right)$ មានតម្លៃធំជាងគេក្នុងចំណោមក្រុមទាំងអស់។

ក្នុងករណីចំណាត់ថ្នាក់ច្រើនក្រុមនេះ យើងកំណត់សរសេរលទ្ធផលពិត$\pmb{t}_n$នៃអថេរ$\pmb{x}_n$ដោយទម្រង់វ៉ិចទ័រ(one-hot vector)$ \pmb{t}_n=\left[\begin{matrix}t_{n1}&\cdots&t_{nk}\\\end{matrix}\right]^\top$។ ក្នុងករណីចំណាត់ថ្នាក់រូបថតលេខសរសេរដោយដៃខាងលើនោះ$K=10$។

បើ$\pmb{x}_n$ ជាលេខ0 ដែលស្ថិតនៅក្នុងក្រុម$\mathcal{C}_1$នោះ $\pmb{t}_n=\left[1\ \ 0\ \ 0\ \ 0\ \ 0\ \ 0\ \ 0\ \ 0\ \ 0\ \ 0\ \right]^\top$ និងបើ$ \pmb{x}_n $ជាលេខ5 ដែលស្ថិតនៅក្នុងក្រុម$\mathcal{C}_6$ នោះ $\pmb{t}_n=\left[0\ \ 0\ \ 0\ \ 0\ \ 0\ \ 1\ \ 0\ \ 0\ \ 0\ \ 0\ \right]^\top$។

ដោយសន្មតសរសេរបែបនេះ យើងអាចបង្ហាញ $p\left(\pmb{t}\middle|\pmb{x}\right)$ ជារួមតាមទម្រង់ខាងក្រោម។

\[ p\left(\pmb{t}\middle|\pmb{x}\right)=\prod_{k=1}^{K}{p\left(\mathcal{C}_k|\pmb{x}\right)^{t_k}} \]

ហេតុនេះចំពោះសំណុំទិន្នន័យសម្រាប់រៀន $\left\{\left(\pmb{x}_n,\pmb{t}_n\right)\right\}_{n=1}^N$ កម្រិតសាកសមនៃទិន្នន័យសម្រាប់រៀន(training data) របស់ប៉ារ៉ាម៉ែត្រ$\pmb{w}$ ត្រូវបានកំណត់ដូចទម្រង់ខាងក្រោម។

\[ L\left(\pmb{w}\right)=\prod_{n=1}^{N}{p\left(\pmb{t}_n\middle|\pmb{x}_n;\pmb{w}\right)}=\prod_{n=1}^{N}\prod_{k=1}^{K}{p\left(\mathcal{C}_k|\pmb{x}\right)^{t_{nk}}}=\prod_{n=1}^{N}\prod_{k=1}^{K}\left(y_k\left(\pmb{x}_n;\pmb{w}\right)\right)^{t_{nk}} \]

ដើម្បីសម្រួលដល់ការធ្វើបរមាកម្ម យើងអនុវត្តអនុគមន៍លោការីតលើកន្សោមខាងលើ។ ក្នុងករណីនេះ អនុគមន៍កម្រិតលម្អៀងនៃចំណោទចំណាត់ថ្នាក់ច្រើនក្រុមកំណត់ដោយ $E\left(\pmb{w}\right)$ ដូចខាងក្រោម។ អនុគមន៍កម្រិតលម្អៀងបែបនេះហៅថា cross entropy ។

\[ E\left(\pmb{w}\right)=-\log{L\left(\pmb{w}\right)}=-\sum_{n=1}^{N}\sum_{k=1}^{K}{t_{nk}\log{y_k\left(\pmb{x}_n;\pmb{w}\right)}} \]

ការប្រើអនុគមន៍Softmax សម្រាប់ជាម៉ូឌែលនៃបំណែងចែកច្រើនថ្នាក់នេះអាចបកស្រាយដូចខាងក្រោម។ ប្រូបាបដែលធាតុចូល $\pmb{x}$ ត្រូវកំណត់ថានៅក្នុងក្រុម$\mathcal{C}_k$ អាចគណនាដោយ

\[ p\left(\mathcal{C}_k|\pmb{x}\right)=\frac{p\left(\pmb{x}|\mathcal{C}_k\right)}{\sum_{i=1}^{K}p\left(\pmb{x}|\mathcal{C}_k\right)} \]

នៅទីនេះដោយតាង $u_k=\log{\left(p\left(\pmb{x},\mathcal{C}_k\right)\right)}$ នោះ $p\left(\pmb{x},\mathcal{C}_k\right)=\exp{\left(u_k\right)} $ ហេតុនេះ

\[ p\left(\mathcal{C}_k|\pmb{x}\right)=\frac{\exp{\left(u_k\right)}}{\sum_{i=1}^{K}\exp{\left(u_i\right)}} \]

កន្សោម$p\left(\mathcal{C}_k|\pmb{x}\right)$ ដែលទាញបានខាងលើនេះដូចគ្នាទៅនឹងអនុគមន៍Softmaxដែរ។

ដូច្នេះភាពត្រឹមត្រូវនៃការប្រើប្រាស់អនុគមន៍Softmax ជាអនុគមន៍សកម្មសម្រាប់ចំណោទចំណាត់ថ្នាក់ច្រើនក្រុមដោយFNNត្រូវបានផ្ទៀងផ្ទាត់។

Machine Learning