Perceptron¶

import numpy as np
import matplotlib.pyplot as plt

ក្នុងអត្ថបទនេះយើងនឹងលើកយក Perceptron Algorithm មកបង្ហាញ។ Perceptron គឺជាAlgorithm មួយដែលត្រូវបានណែនាំជាដំបូងដោយអ្នកស្រាវជ្រាវអាមេរិកគឺលោក Alexander Rosenblatt នៅឆ្នាំ១៩៥៧។ ទោះបីជាPerceptron Algorithm ជាវិធីសាស្រ្តចាស់ក្តី ប៉ុន្តែជាត្រូវបានគេស្គាល់ថាជាប្រភពដើមនៃវិធីសាស្រ្តគណនាក្នុងម៉ូឌែលNeural Network ឬ Deep Learningដែលកំពុងរីកដុះដាលយ៉ាងសកម្មនាសម័យនេះ។ ហេតុនេះ ការសិក្សាអំពីPerceptron Algorithm អាចជួយឱ្យយើងងាយស្រួលក្នុងការឈានទៅសិក្សាអំពីNeural Network ឬ Deep Learning។

អំពីPerceptron¶

Perceptron ឬហៅថាម៉ូឌែលណឺរ៉ូនសិប្បនិម្មិត(artificial neuron) ជាម៉ូឌែលគណិតវិទ្យា មួយដែលទទួលសញ្ញាណ(signal)ឬ ធាតុចូល(input)ច្រើន និងផ្តល់នូវលទ្ធផល(output)មួយ។សញ្ញាណដែលទទួលនៅទីនេះអាចប្រៀបបានជាចរន្តអគ្គិសនីឬសញ្ញាណព័ត៌មានដូចដែលណឺរ៉ូននៃប្រព័ន្ធប្រសាទរបស់ភាវរស់ទទួលដែរ។ ប៉ុន្តែសញ្ញាណឬធាតុចូលក្នុងPerceptron កត់យកតម្លៃធម្មតាពោលគឺបញ្ជូនបន្តឬមិនបញ្ជូនបន្តដោយតម្លៃ(1 ឬ 0)។

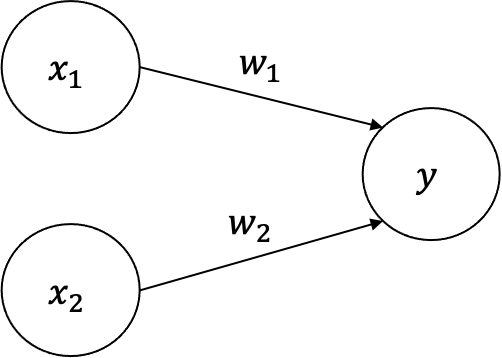
រូបខាងក្រោមបង្ហាញអំពីPerceptronដែលទទួលសញ្ញាណឬធាតុចូល(input) 2។ រង្វង់ដែលមានក្នុងរូបហៅថាណឺរ៉ូន(neuron) ឬnode។ \(x_1,x_2\) ជាសញ្ញាណឬធាតុចូល ឯ\(y\) គឺជាលទ្ធផលនៃណឺរ៉ូននោះ។ \(w_1, w_2\) ជាទម្ងន់ផ្ទាល់នៃណឺរ៉ូនចំពោះធាតុចូលនិមួយៗ ពោលគឺតម្លៃដែលបង្ហាញនូវកម្រិតឥទ្ធិពលនៃធាតុចូលនិមួយៗទៅលើលទ្ធផល។ តម្លៃនៃទម្ងន់កាន់តែធំបង្ហាញពីកម្រិតសំខាន់នៃធាតុចូលនោះ។

នៅពេលដែលណឺរ៉ូនមួយទទួលបាននូវសញ្ញាណឬធាតុចូល នោះផលគុណរវាងតម្លៃនៃធាតុចូលនោះនិងតម្លៃនៃទម្ងន់ផ្ទាល់របស់ណឺរ៉ូននោះ\((w_1x_1,w_2x_2)\)ត្រូវបានគណនា។ លទ្ធផលដែលណឺរ៉ូននោះត្រូវផ្តល់គឺអាស្រ័យនឹងផលបូកនៃគ្រប់ធាតុចូលទាំងអស់ ដោយកំណត់តាមលក្ខខណ្ឌខាងក្រោម។ លក្ខខណ្ឌនេះគឺ ណឺរ៉ូននឹងបញ្ចេញលទ្ធផល 1 បើផលបូកនៃផលគុណធាតុចូលនិងទម្ងន់របស់វាធំជាងតម្លៃនៃកម្រិតកំណត់របស់ណឺរ៉ូន ឬ បញ្ចេញលទ្ធផល 0 បើតូចជាង។ តម្លៃនៃកម្រិតកំណត់របស់ណឺរ៉ូនហៅថា Threshold។ នៅទីនេះ \(\theta\) ជាតម្លៃThreshold ។

\[\begin{split} y=\left\{\begin{matrix} 1 & (w_1x_1+w_2x_2 > \theta)\\ 0 & (w_1x_1+w_2x_2 \leq \theta) \end{matrix}\right. \end{split}\]

perceptron

ក្នុងការអនុវត្តភាគច្រើន គេច្រើនបម្លែងទម្រង់ខាងលើជាទម្រង់ដែលមានកម្រិតកំណត់នៃណឺរ៉ូនស្មើ០ ដោយហៅតម្លៃ\( \theta \)ដែលត្រូវបានបញ្ជូនទៅអង្គទី១\(\left(b=-\theta\right)\) ដោយ bias ។

\[\begin{split} y=\left\{\begin{matrix} 1 &(b+w_1x_1+w_2x_2>0)\\ 0 &(b+w_1x_1+w_2x_2\leq 0) \end{matrix}\right. \end{split}\]

បង្ហាញសៀគ្វីឡូស៊ីកងាយៗដោយម៉ូឌែលPerceptron¶

ដើម្បីស្វែងយល់អំពីដំណើរការរបស់Perceptron នៅទីនេះយើងលើកយកសៀគ្វីឡូស៊ីក(Logic circuits) ងាយៗដូចជា AND gate, OR gate មកបង្ហាញដោយប្រើម៉ូឌែលPerceptron។

AND gate¶

ដូចដែលអ្នកបានដឹង AND gate ផ្តល់នូវលទ្ធផលអាស្រ័យនឹងតម្លៃភាពពិតនៃធាតុចូលរបស់វាដូចក្នុងតារាងខាងក្រោម។

\(x_1\)	\(x_2\)	\(y=x_1 \wedge x_2\)
0	0	0
0	1	0
1	0	0
1	1	1

X = np.array([(0,0),(1,0),(0,1),(1,1)])
y = np.array([0,0,0,1])
w = [0.5,0.5,0.8]

plt.scatter(X[y==0,0],X[y==0,1],c='b',s=100,label='0')
plt.scatter(X[y==1,0],X[y==1,1],c='g',s=100,label='1')
xx = np.linspace(-1,1.5,100)
plt.plot(xx,-w[0]/w[1]*xx+w[2]/w[1],c='r')
plt.xlim([-0.5,1.5])
plt.ylim([-0.5,1.5])
plt.grid()
plt.title("AND gate")
plt.legend()
plt.show()

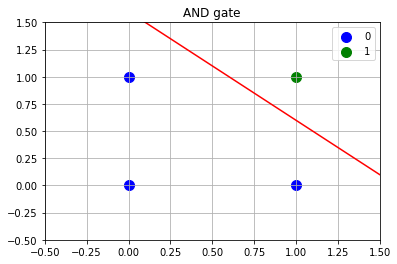
ក្នុងករណីនេះ បើយើងយកPerceptronមួយដែលទទួលធាតុចូលពីរនិងមានតម្លៃទម្ងន់និងកម្រិតកំណត់(threshold)

\[ \left(w_1,w_2,\theta\right)=\left(0.5,\ 0.5,\ 0.8\right) \]

នោះយើងអាចបង្ហាញAND gateដោយPerceptronបាន។

ឧទាហរណ៍ ករណី \(\left(x_1,x_2\right)=\left(1,0\right)\) នោះ \(w_1x_1+w_2x_2=0.5<0.8\) ហេតុនេះ \(y=0\)។

ករណី \(\left(x_1,x_2\right)=\left(1,1\right)\) នោះ \(w_1x_1+w_2x_2=1>0.8\) ហេតុនេះ \(y=1\)។

OR gate¶

OR gate ផ្តល់នូវលទ្ធផលអាស្រ័យនឹងតម្លៃភាពពិតនៃធាតុចូលរបស់វាដូចក្នុងតារាងខាងក្រោម។

\(x_1\)	\(x_2\)	\(y=x_1 \vee x_2\)
0	0	0
0	1	1
1	0	1
1	1	1

X = np.array([(0,0),(1,0),(0,1),(1,1)])
y = np.array([0,1,1,1])
w = [0.5,0.5,0.2]

plt.scatter(X[y==0,0],X[y==0,1],c='b',s=100,label='0')
plt.scatter(X[y==1,0],X[y==1,1],c='g',s=100,label='1')
xx = np.linspace(-1,1.5,100)
plt.plot(xx,-w[0]/w[1]*xx+w[2]/w[1],c='r')
plt.xlim([-0.5,1.5])
plt.ylim([-0.5,1.5])
plt.grid()
plt.title("OR gate")
plt.legend()
plt.show()

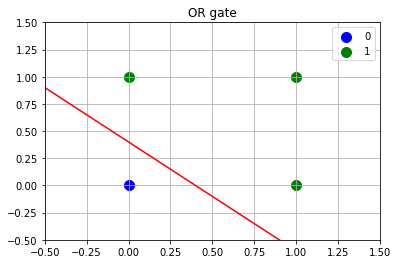
ក្នុងករណីនេះ បើយើងយកPerceptronមួយដែលទទួលធាតុចូលពីរនិងមានតម្លៃទម្ងន់និងកម្រិតកំណត់(threshold)

\[ \left(w_1,w_2,\theta\right)=\left(0.5,\ 0.5,\ 0.2\right) \]

នោះយើងអាចបង្ហាញOR gateដោយPerceptronបាន។

ឧទាហរណ៍ ករណី \(\left(x_1,x_2\right)=\left(1,0\right)\) នោះ \(w_1x_1+w_2x_2=0.5>0.2\) ហេតុនេះ \(y=1\)។

ករណី \(\left(x_1,x_2\right)=\left(0,0\right)\) នោះ \(w_1x_1+w_2x_2=0<0.2\) ហេតុនេះ \(y=0\)។

ដូចដែលបង្ហាញខាងលើ ដោយប្រើPerceptronយើងអាចបង្ហាញសៀគ្វីឡូស៊ីកងាយៗបាន។ ចំណុចសំខាន់នៅទីនេះគឺ ចំពោះAND gate, OR gate ដែលមានទម្រង់សៀគ្វីឡូស៊ីកផ្សេងៗគ្នាក្តី Perceptronដែលយើងប្រើមានគោលគំនិតឬទម្រង់តែមួយមិនប្រែប្រួលឡើយ។ អ្វីដែលខុសគ្នាគឺតម្លៃនៃប៉ារ៉ាម៉ែត្រ(ទម្ងន់និងកម្រិតកំណត់របស់ណឺរ៉ូន)តែប៉ុណ្ណោះ។ ពោលគឺដោយប្រើទម្រង់នៃម៉ូឌែលតែមួយយើងអាចបង្ហាញទម្រង់នៃសៀគ្វីឡូស៊ីកដែលជាគ្រឹះនៃសៀគ្វីអេឡិចត្រូនិចនានាបានដោយគ្រាន់តែកែសម្រួលតម្លៃនៃប៉ារ៉ាម៉ែត្ររបស់វាតែប៉ុណ្ណោះ។

ព្រំដែនសមត្ថភាពនៃPerceptron¶

យើងឃើញថាPerceptron អាចបង្ហាញ AND gate, OR gateបានយ៉ាងងាយ។ បន្តទៅនេះយើងនឹងពិនិត្យលើករណីនៃ XOR gate។

\(x_1\)	\(x_2\)	\(y=x_1 \oplus x_2\)
0	0	0
0	1	1
1	0	1
1	1	0

X = np.array([(0,0),(1,0),(0,1),(1,1)])
y = np.array([0,1,1,0])

plt.scatter(X[y==0,0],X[y==0,1],c='b',s=100,label='0')
plt.scatter(X[y==1,0],X[y==1,1],c='g',s=100,label='1')
plt.xlim([-0.5,1.5])
plt.ylim([-0.5,1.5])
plt.grid()
plt.title("XOR gate")
plt.legend()
plt.show()

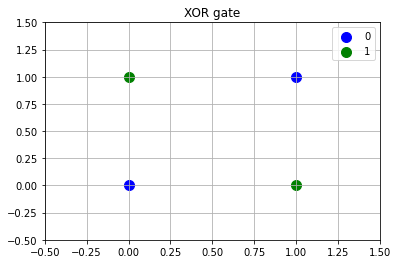
មុននឹងឈានទៅមើលករណីXOR gate យើងបង្ហាញព្រមគ្នាជាមួយករណីOR gateដោយប្រើក្រាបដូចរូបទី២។ ក្នុងករណី OR gate យើងអាចកំណត់តម្លៃប៉ារ៉ាម៉ែត្ររបស់Perceptronបានដូចឧទាហរណ៍ក្នុងចំណុច2. ដែលលទ្ធផល1 ឬ 0 អាចបែងចែកដាច់ពីគ្នាបានដោយបន្ទាត់ត្រង់មួយបាន។ ផ្ទុយពីនេះ ករណី XOR gate យើងមិនអាចកំណត់បន្ទាត់ត្រង់ដើម្បីបែងចែកករណីលទ្ធផល1 ឬ 0 បានឡើយ។ ពោលគឺមិនអាចកំណត់ប៉ារ៉ាម៉ែត្រណាដែលអាចឱ្យPerceptronបង្ហាញXOR gate បានទេ។

ទិន្នន័យដូចក្នុងករណីOR gate ហៅថាទិន្នន័យដែលអាចបែងចែកលីនេអ៊ែរបាន(linear seperable) ឯទិន្នន័យដូចក្នុងករណីXOR gate ហៅថាទិន្នន័យដែលមិនអាចបែងចែកលីនេអ៊ែរបាន(linear non-seperable)។ ហេតុនេះ យើងអាចនិយាយបានថា Perceptronដែលមានទម្រង់ដូចណែនាំក្នុងចំណុច1. មិនអាចប្រើជាម៉ូឌែលសម្រាប់ទិន្នន័យមិនអាចបែងចែកលីនេអ៊ែរបានល្អឡើយ។

Perceptronច្រើនថ្នាក់ (Multilayer Perceptron)¶

ដូចដែលបានពិនិត្យខាងលើ Perceptronទម្រង់ធម្មតាមិនអាចធ្វើការពណ៌នាXOR gate បានប្រសើរឡើយ។ ដើម្បីស្វែងយល់ពីដំណោះស្រាយតាមរយៈការបង្កើនចំនួនថ្នាក់នៃPerceptronយើងពិនិត្យលើការបង្ហាញទម្រង់XOR gate ដោយប្រើបង្គុំនៃសៀគ្វីឡូស៊ីកមូលដ្ឋានAND gate, OR gate, NAND gate។

បង្ហាញXOR gate ដោយប្រើ AND gate, OR gate, NAND gate¶

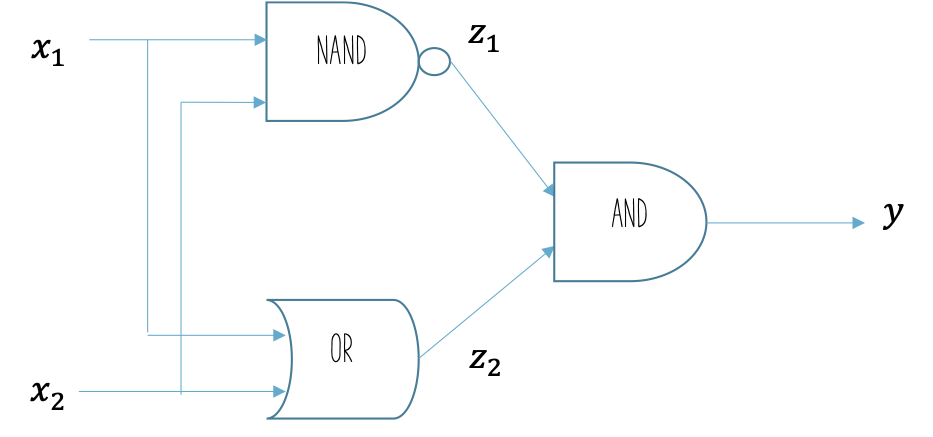
នៅទីនេះយើងនឹងមិនធ្វើការបកស្រាយលំអិតអំពីលក្ខណៈនៃសៀគ្វីឡូស៊ីកឡើយ ប៉ុន្តែ តាមពិតទៅXOR gate អាចបង្ហាញដោយប្រើ AND gate, OR gate, NAND gateបានដោយធ្វើតំណភ្ជាប់ដូចរូបខាងក្រោម។ ដោយសារតែAND gate, OR gate, NAND gate អាចបង្ហាញដោយប្រើPerceptron ទម្រង់ធម្មតាដូចក្នុងចំណុច1. 2.ខាងលើបាន ហេតុនេះ គំនិតសំខាន់ដែលយើងអាចសិក្សាពីចំណុចនេះគឺថា យើងអាចផ្គុំPerceptronធម្មតាជាច្រើនថ្នាក់ដើម្បីបង្ហាញXOR gateបាន។

perceptron-2

def AND(x1, x2):
  (w1,w2,theta) = (0.5, 0.5, 0.8)
  t = w1*x1 + w2*x2 
  y = 1 if t > theta else 0
  return y

def OR(x1, x2):
  (w1,w2,theta) = (0.5, 0.5, 0.2)
  t = w1*x1 + w2*x2 
  y = 1 if t > theta else 0
  return y

def NAND(x1, x2):
  (w1,w2,theta) = (-0.5, -0.5, -0.8)
  t = w1*x1 + w2*x2 
  y = 1 if t > theta else 0
  return y

print("x_1  :",0,0,1,1)
print("x_2  :",0,1,0,1)
print("OR   :",OR(0,0),OR(0,1),OR(1,0),OR(1,1))
print("AND  :",AND(0,0),AND(0,1),AND(1,0),AND(1,1))
print("NAND :",NAND(0,0),NAND(1,0),NAND(0,1),NAND(1,1))

x_1  : 0 0 1 1
x_2  : 0 1 0 1
OR   : 0 1 1 1
AND  : 0 0 0 1
NAND : 1 1 1 0

# with bias
def AND(x1, x2):
  x_vec = np.array([x1,x2])
  w = np.array([0.5,0.5])
  b = -0.8
  t = np.sum(w*x_vec) + b
  y = 1 if t > 0 else 0
  return y

def OR(x1, x2):
  x_vec = np.array([x1,x2])
  w = np.array([0.5,0.5])
  b = -0.2
  t = np.sum(w*x_vec) + b
  y = 1 if t > 0 else 0
  return y

def NAND(x1, x2):
  x_vec = np.array([x1,x2])
  w = np.array([-0.5,-0.5])
  b = 0.8
  t = np.sum(w*x_vec) + b
  y = 1 if t > 0 else 0
  return y

print("x_1  :",0,0,1,1)
print("x_2  :",0,1,0,1)
print("OR   :",OR(0,0),OR(0,1),OR(1,0),OR(1,1))
print("AND  :",AND(0,0),AND(0,1),AND(1,0),AND(1,1))
print("NAND :",NAND(0,0),NAND(1,0),NAND(0,1),NAND(1,1))

x_1  : 0 0 1 1
x_2  : 0 1 0 1
OR   : 0 1 1 1
AND  : 0 0 0 1
NAND : 1 1 1 0

def XOR(x1,x2):
  s1 = NAND(x1,x2)
  s2 = OR(x1,x2)
  y = AND(s1,s2)
  return y

print("x_1  :",0,0,1,1)
print("x_2  :",0,1,0,1)
print("XOR  :",XOR(0,0),XOR(0,1),XOR(1,0),XOR(1,1))

x_1  : 0 0 1 1
x_2  : 0 1 0 1
XOR  : 0 1 1 0

ទម្រង់នៃXOR gateដោយបង្គុំនៃAND gate, OR gate, NAND gateដូចក្នុងរូបទី៣ អាចប្រដូចបានជាករណីមួយនៃករណីទូទៅរបស់បង្គុំនៃPerceptronទម្រង់ធម្មតាច្រើនបញ្ចូលគ្នាដូចក្នុងរូបទី៤។ ទម្រង់បែបនេះហៅថា Multilayer Perceptron ដែលក្នុងអត្ថបទនេះនិងបន្តបន្ទាប់យើងកំណត់ហៅថា Perceptronច្រើនថ្នាក់។

ដូចក្នុងករណីXOR gate ដែរ ការប្រើMultilayer Perceptronអាចឱ្យយើងបង្ហាញទិន្នន័យដែលមិនអាចបែងចែកលីនេអ៊ែរដោយម៉ូឌែលPerceptronបាន។ ការបង្កើនចំនួនថ្នាក់(Layer)ក្នុងPerceptronនឹងជួយបង្កើនសមត្ថភាពរបស់វាក្នុងការពណ៌នាលក្ខណៈរបស់ទិន្នន័យដែលកាន់តែស្មុគស្មាញបានដែលនេះជាគោលគំនិតគ្រឹះក្នុង Artificial Neural Network ឬ Deep Learningដែលយើងនឹងលើកមកសិក្សាក្នុងអត្ថបទក្រោយៗ។

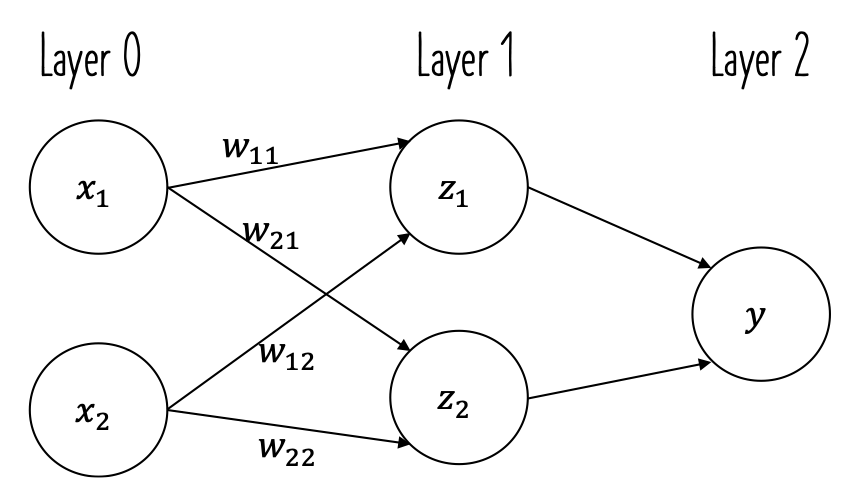
perceptron-3

ការកំណត់ប៉ារ៉ាម៉ែត្រនៃPerceptron ១ថ្នាក់(Perceptron Algorithm)¶

ចំពោះPaceptronទម្រង់ធម្មតា១ថ្នាក់ យើងអាចកំណត់តម្លៃនៃប៉ារ៉ាម៉ែត្រពីទិន្នន័យដែល មានបានដោយអនុវត្តតាមវិធីសាស្រ្តខាងក្រោម។នៅទីនេះ\(\pmb{w}^{\left(t\right)}\)សម្គាល់តម្លៃនៃប៉ារ៉ាម៉ែត្រនៅដំណាក់កាលផ្លាស់ប្តូរទី\(t , \eta\) សម្គាល់តម្លៃនៃកម្រិតផ្លាស់ប្តូរប៉ារ៉ាម៉ែត្រដែលហៅថា learning rate។

(ជំហានទី១) កំណត់តម្លៃដើមនៃប៉ារ៉ាម៉ែត្រ \(\pmb{w}\) ដោយ 0 ឬតម្លៃពីបំណែងចែកចៃដន្យ

(ជំហានទី២) ចំពោះទិន្នន័យ(training data) \(\left(\pmb{x}_i,y_i\right)\) អនុវត្តជំហានខាងក្រោមរហូតដល់គ្មាន កំហុសក្នុងការប៉ាន់ស្មានតម្លៃ ពោលគឺ \(\mathbf{\Delta}\pmb{w}^{\left(t\right)}=\mathbf{0}\)

ក. គណនាលទ្ធផលនៃណឺរ៉ូនដោយប្រើតម្លៃប៉ារ៉ាម៉ែត្របច្ចុប្បន្ន

\[ {\hat{y}}_i=\pmb{x}_i^\top\pmb{w}^{\left(t\right)} \]

ខ. ផ្លាស់ប្តូរតម្លៃនៃប៉ារ៉ាម៉ែត្រ

\[ \pmb{w}^{\left(t+1\right)}=\pmb{w}^{\left(t\right)}+\mathbf{\Delta}\pmb{w}^{\left(t\right)} \]

\[ \mathbf{\Delta}\pmb{w}^{\left(t\right)}=\eta\left(y_i-{\hat{y}}_i\right)\pmb{x}_i \]

class Perceptron(object):
  def __init__(self, learning_rate=0.01, iteration_number=100, random_state=100):
    self.eta = learning_rate
    self.n_iteration = iteration_number
    self.random_state = random_state
  
  # learning process
  def fit(self, X, y):
    rand_gen = np.random.RandomState(self.random_state)
    self.w = rand_gen.normal(loc=0.0, scale=0.1, size=1+X.shape[1])
    self.errors = []
    XP = np.ones((X.shape[0],X.shape[1]+1))
    XP[:,:-1]=X

    for t in range(self.n_iteration):
      error = 0
      for xi,yi in zip(XP,y):
        delta = self.eta * (yi - self.predict(xi))
        self.w += delta * xi
        error += int(delta != 0.0)
      self.errors.append(error)
    return self

  def predict(self, X):
    z = X@self.w
    return np.where(z >= 0.0, 1, 0)

ពិនិត្យឡើងវិញករណី AND, OR

X = np.array([[0,0],[0,1],[1,0],[1,1]])
y = np.array([0,0,0,1])

model = Perceptron(learning_rate=0.01, iteration_number=25)
model.fit(X,y)
print("parameter: ",model.w)

parameter:  [ 0.01502345  0.01426804 -0.02469642]

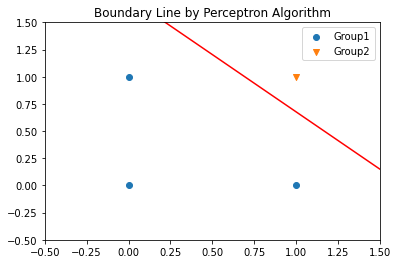
plt.scatter(X[y==0,0],X[y==0,1],marker='o',label='Group1')
plt.scatter(X[y==1,0],X[y==1,1],marker='v',label='Group2')
xx_ = np.linspace(X.min()-0.5,X.max()+0.5,50)
plt.plot(xx_,-(xx_*model.w[0]+model.w[-1])/model.w[1],'r-')
plt.xlim([-0.5,1.5]);plt.ylim([-0.5,1.5])
plt.legend()
plt.title("Boundary Line by Perceptron Algorithm")
plt.show()

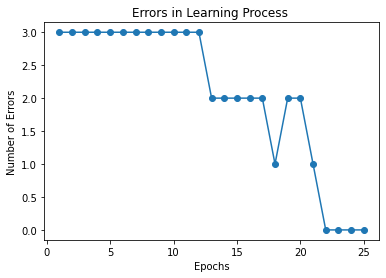
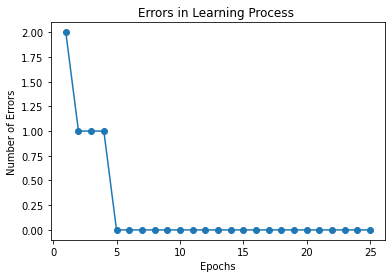
plt.plot(range(1,len(model.errors)+1), model.errors, marker='o')
plt.xlabel('Epochs')
plt.ylabel('Number of Errors')
plt.title("Errors in Learning Process ")
plt.show()

X = np.array([[0,0],[0,1],[1,0],[1,1]])
y = np.array([0,1,1,1])

model = Perceptron(learning_rate=0.01, iteration_number=25, random_state=10)
model.fit(X,y)
print("parameter: ",model.w)

parameter:  [ 0.14315865  0.1115279  -0.10454003]

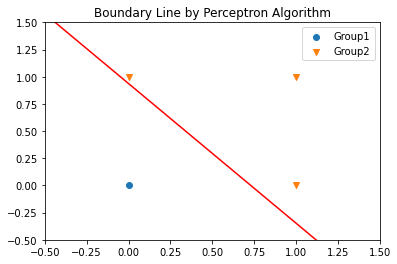
plt.scatter(X[y==0,0],X[y==0,1],marker='o',label='Group1')
plt.scatter(X[y==1,0],X[y==1,1],marker='v',label='Group2')
xx_ = np.linspace(X.min()-0.5,X.max()+0.5,50)
plt.plot(xx_,-(xx_*model.w[0]+model.w[-1])/model.w[1],'r-')
plt.xlim([-0.5,1.5]);plt.ylim([-0.5,1.5])
plt.legend()
plt.title("Boundary Line by Perceptron Algorithm")
plt.show()

plt.plot(range(1,len(model.errors)+1), model.errors, marker='o')
plt.xlabel('Epochs')
plt.ylabel('Number of Errors')
plt.title("Errors in Learning Process ")
plt.show()

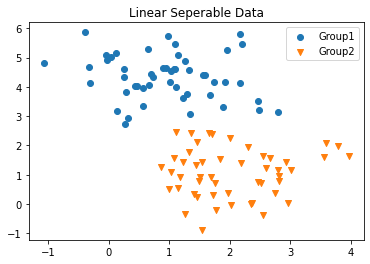
ករណីទិន្នន័យអាចបែងចែកលីនេអ៊ែរបាន

from sklearn.datasets import make_blobs

X,y = make_blobs(n_samples=100, n_features=2, cluster_std=0.8, centers=2, random_state=0)

plt.scatter(X[y==0,0],X[y==0,1],marker='o',label='Group1')
plt.scatter(X[y==1,0],X[y==1,1],marker='v',label='Group2')
plt.legend()
plt.title("Linear Seperable Data")
plt.show()

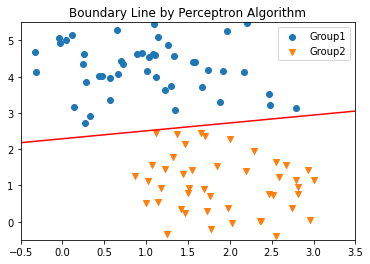
model = Perceptron(learning_rate=0.01, iteration_number=25, random_state=10)
model.fit(X,y)

plt.scatter(X[y==0,0],X[y==0,1],marker='o',label='Group1')
plt.scatter(X[y==1,0],X[y==1,1],marker='v',label='Group2')
xx_ = np.linspace(X.min(),X.max(),50)
plt.plot(xx_,-(xx_*model.w[0]+model.w[-1])/model.w[1],'r-')
plt.xlim([-0.5,3.5]);plt.ylim([-0.5,5.5])
plt.legend()
plt.title("Boundary Line by Perceptron Algorithm")
plt.show()

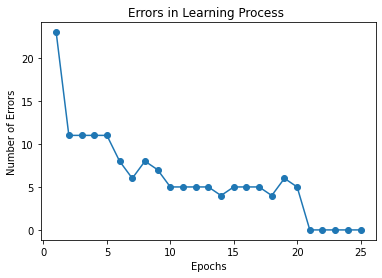
plt.plot(range(1,len(model.errors)+1), model.errors, marker='o')
plt.xlabel('Epochs')
plt.ylabel('Number of Errors')
plt.title("Errors in Learning Process ")
plt.show()

Machine Learning