វិធីសាស្រ្តបរមាកម្មតាមរយៈ SGD¶
ក្នុងមេរៀនមុនយើងបានសិក្សាអំពីម៉ូឌែលតម្រែតម្រង់លីនេអ៊ែរ ដែលត្រូវបានប្រើប្រាស់សម្រាប់សិក្សាពីការទំនាក់ទំនងរវាងអថេរពន្យល់និងអថេរគោលដៅ។ ក្នុងការកំណត់តម្លៃប៉ារ៉ាម៉ែត្រនៃម៉ូឌែល(មេគុណតម្រែតម្រង់) យើងបានដោះស្រាយតាមរយៈវិធីសាស្រ្តជាមូលដ្ឋាននៃគណិតវិទ្យាវិភាគ។
ប៉ុន្តែក្នុងជីវភាពរស់នៅ ករណីភាគច្រើនចំនួននៃអថេរពន្យល់មានចំនួនច្រើនលើសលប់ ដែលធ្វើឱ្យវិមាត្រនៃម៉ាទ្រីសផែនការមានការកើនឡើងខ្ពស់។ ហេតុនេះ វាមានការលំបាកក្នុងការគណនាម៉ាទ្រីសច្រាស់ដូចក្នុងរបៀបខាងលើទោះបីប្រើប្រាស់ម៉ាស៊ីនកុំព្យូទ័រក្តី។
ក្នុងអត្ថបទនេះ យើងនឹងណែនាំវិធីសាស្រ្តកំណត់តម្លៃប៉ាន់ស្មាននៃមេគុណតម្រែតម្រង់ដោយវិធីគណនាដដែលៗលើតម្លៃលេខតាមប្រមាណវិធីងាយៗគឺ Stochastic Gradient Descent (SGD) ។ ដើម្បីងាយស្រួលស្វែងយល់អំពីSGD ជាដំបូងយើងនឹងណែនាំអំពីគំនិត និងការគណនាក្នុងវិធីសាស្រ្ត Gradient Descent ជាមុន។
Gradient Descent¶
ដូចដែលបានបង្ហាញក្នុងអត្ថបទមុន យើងចង់កំណត់យកមេគុណតម្រែតម្រង់ណាដែលធ្វើឱ្យតម្លៃផលបូកការេនៃកម្រិតលម្អៀងតូចបំផុត។ គោលគំនិតក្នុងGradient Descent គឺផ្លាស់ប្តូរតម្លៃនៃមេគុណតម្រែតម្រង់(ប៉ារ៉ាម៉ែត្រ) បន្តិចម្តងៗ ទៅតាមទិសដៅដែលធ្វើឱ្យតម្លៃផលបូកការេនៃកម្រិតលម្អៀងមានការថយចុះ។ អ្នកអាចប្រដូចវិធីនេះទៅនឹងការចុះជំរាលឬចុះពីទីភ្នំ ដោយរំកិលខ្លួនអ្នកបន្តិចម្តងៗ ទៅកាន់ទីដែលទាបជាងកន្លែងដែលអ្នកនៅ។ នៅពេលដែលអ្នករំកិលខ្លួនដល់ទីដែលលែងមានបម្រែបម្រួលនៃរយៈកម្ពស់ អ្នកអាចសន្និដ្ឋានបានថាអ្នកដល់ទីដែលទាបបំផុតហើយ។ ដូចគ្នានេះដែរ នៅក្នុងវិធីសាស្រ្តGradient Descent តាមលក្ខណៈគណិតវិទ្យានៃ gradient (តម្លៃដេរីវេនៃអនុគមន៍ត្រង់ចំនុចណាមួយ) តម្លៃgradientត្រង់ចំណុចណាមួយគឺជាតម្លៃមេគុណប្រាប់ទិសនៃខ្សែកោងត្រង់ចំណុចនោះហើយក៏ជាតម្លៃធំបំផុតនៃបម្រែបម្រួលតម្លៃអនុគមន៍ពេលអ្នកធ្វើបម្រែបម្រួលលើអថេរមិនអាស្រ័យ។

រូបខាងលើនេះបង្ហាញអំពីគំនិតក្នុងវិធីសាស្រ្តធ្វើអប្បបរមាកម្មតាម Gradient Descent។ ដូចដែលអ្នកអាចធ្វើការកត់សម្គាល់បាន ពេលខ្លះអ្នកអាចនឹងធ្លាក់ចុះទៅក្នុងទីតាំងដែលជាបរមាធៀបតែមិនមែនជាកន្លែងអប្បបរមាពិតប្រាកដប្រសិនបើទីតាំងនៃការចាប់ផ្តើមរបស់អ្នកមិនប្រសើរ។ ប៉ុន្តែក្នុងករណីធ្វើបរមាកម្មតម្លៃផលបូកការេនៃកម្រិតលម្អៀងរបស់យើង ដោយសារអនុគមន៍ដែលត្រូវធ្វើបរមាកម្មគឺជាអនុគមន៍ដឺក្រេទី២ ហេតុនេះយើងមិនមានការព្រួយបារម្ភក្នុងករណីនេះឡើយ។
ពេលនេះ យើងពិនិត្យលើការគណនាក្នុងវិធីសាស្រ្ត Gradient Descent។
យើងសិក្សាលើអនុគមន៍ដែលយកតម្លៃស្កាលែ \(f\left(\pmb{x}\right)\) ដែល \(\pmb{x}\in\mathbb{R}^d\)។ សន្មតថាអនុគមន៍នេះយកតម្លៃអប្បបរមាត្រង់ចំណុច \(\pmb{x}^\ast\) ។ វិធីសាស្រ្ត Gradient Descent អាចឱ្យយើងគណនាតម្លៃ(ប្រហែល)នៃ \(\pmb{x}^\ast\) បានដោយចាប់ផ្តើមពីតម្លៃ\(\ \pmb{x}^{\left(0\right)}\ \)ណាមួយ រួចធ្វើការផ្លាស់ប្តូរតម្លៃនេះតាមការគណនាដូចខាងក្រោម។
នៅទីនេះ\(t=0,1,\ldots\) គឺជាលេខរៀងនៃការផ្លាស់ប្តូរតម្លៃអថេរ\(\pmb{x}\)។ \(\frac{\partial f\left(\pmb{x}\right)}{\partial\pmb{x}} \) គឺជាដេរីវេដោយផ្នែកនៃអនុគមន៍\(\ f \)ធៀបនឹងអថេរ\( \pmb{x} \)ឬហៅថា gradient ។\( \eta_t \)គឺជាកម្រិតនៃការផ្លាស់ប្តូរតម្លៃអថេរដោយគ្រប់គ្រងលើឥទ្ធិពលនៃតម្លៃgradient។ នៅក្នុង Machine Learning វាត្រូវបានហៅថាជា អត្រារៀនឬ learning rate ។ ជាទូទៅតម្លៃនៃ\(\eta_t\) ត្រូវបានកំណត់យកចន្លោះ០និង១ដោយតម្លៃយ៉ាងតូច។ យើងអាចកំណត់លក្ខខណ្ឌសម្រាប់បញ្ចប់ការផ្លាស់ប្តូរតម្លៃនៃអថេរបាន ដោយយកពេលដែលតម្លៃដាច់ខាតនៃ gradient យកតម្លៃសូន្យឬក្បែរសូន្យ។
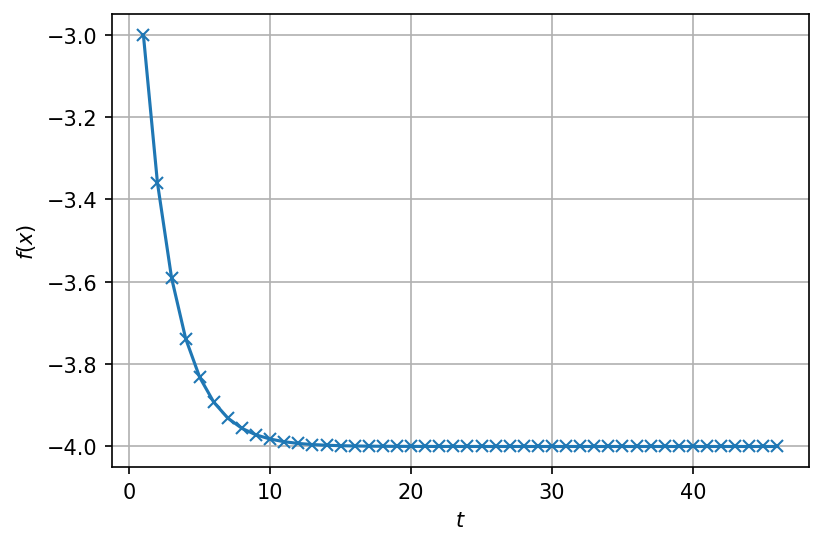
ពិនិត្យលើករណីគម្រូងាយមួយ \(f\left(x\right)=x^2-2x-3 \)។ ករណីនេះយើងដឹងច្បាស់ថាតម្លៃអប្បបរមានៃអនុគមន៍គឺ \(-4\) នៅពេលដែល \(x^\ast=1\)។ យើងនឹងផ្ទៀងផ្ទាត់ជាមួយតម្លៃដែលគណនាតាមរយៈGradient Descent។
ដំបូងយើងគណនាអនុគមន៍ដេរីវេ \( \frac{df\left(x\right)}{dx}=2x-2 \)និង កំណត់យកអត្រា\(\ \eta=0.1 \)ថេរ។ យើងចាប់ផ្តើមពីចំណុច\( x^{\left(0\right)}=0\ \ ,\ f\left(x^{\left(0\right)}\right)=-3 \)។ ដោយផ្លាស់ប្តូរតម្លៃអថេរតាមរយៈGradient Descent ខាងលើយើងបានបម្រែបម្រួលនៃតម្លៃអថេរនិងតម្លៃអនុគមន៍ដូចតារាងខាងក្រោម។
\(\pmb{t}\) |
\(x^{(t)}\) |
\( \frac{df\left(x\right)}{dx}\) |
\(f(x) \) |
|---|---|---|---|
0 |
0.00 |
-2.00 |
-3.00 |
1 |
0.20 |
-1.60 |
-3.36 |
2 |
0.36 |
-1.28 |
-3.59 |
\(\vdots\) |
\(\vdots\) |
\(\vdots\) |
\(\vdots\) |
44 |
0.999946 |
-0.000109 |
-4.00 |
45 |
0.999956 |
-0.000087 |
-4.00 |
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return x ** 2 - 2 * x -3
def g(x):
return 2*x - 2
def sd(f, g, x=0., eta=0.01, eps=1e-4):
t = 1
H = []
while True:
gx = g(x)
H.append(dict(t=t, x=x, fx=f(x), gx=gx))
if -eps < gx < eps:
break
x -= eta * gx
t += 1
return H
H = sd(f, g, x = 0, eta=0.1)
H[-1]
{'t': 46,
'x': 0.9999564438570341,
'fx': -3.9999999981028624,
'gx': -8.711228593183407e-05}
fig = plt.figure(dpi=150)
ax = fig.add_subplot(1,1,1)
ax.plot(
[h['t'] for h in H],
[h['fx'] for h in H],
'x-'
)
ax.set_xlabel('$t$')
ax.set_ylabel('$f(x)$')
ax.grid()
យើងត្រលប់ទៅកាន់ម៉ូឌែលតម្រែតម្រង់របស់យើងវិញ។ អនុគមន៍ដែលយើងចង់ធ្វើអប្បបរមាកម្មគឺ \(E\left(\pmb{\beta}\right)\) ដោយយក\(\ \pmb{\beta} \)ជាអថេរ។
អនុគមន៍ដេរីវេ(gradient)របស់វាគឺ
ហេតុនេះ កន្សោមសម្រាប់ការផ្លាស់ប្តូរតម្លៃអថេរគឺ
ដែល\(\hat{\pmb{y}}^{\left(t\right)}=X\pmb{\beta}^{\left(t\right)}\)។
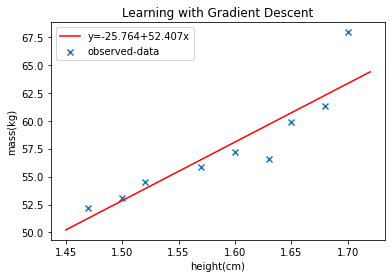
យើងសាកល្បងគណនាតម្លៃប្រហែលនៃមេគុណតម្រែតម្រង់ដែលបានសិក្សាក្នុងអត្ថបទមុនដោយប្រើ gradient descent។ លើកនេះយើងយកតម្លៃកម្ពស់គិតជាម៉ែត្រដើម្បីបង្រួមតម្លៃលេខ។
|
|
|
|
|
|
|
|
|
|
|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
X = np.array([1.52,1.57,1.60,1.63,1.50,1.47,1.65,1.68,1.70])
y = np.array([54.48,55.84,57.20,56.57,53.12,52.21,59.93,61.29,67.92])
XP = np.vstack([np.ones_like(X), X]).T
beta = np.zeros(XP.shape[1])
eta = 1e-3
for t in range(100000):
y_hat = XP @ beta
beta -= 2 * eta * XP.T @ (y_hat - y)
def predict(x,w,k):
X_ = np.zeros((len(x),k+1))
for i in range(k+1):
X_[:,i] = x**i
return X_@w
xa = np.linspace(1.45,1.72,50)
plt.scatter(X,y,marker='x')
plt.plot(xa,predict(xa,beta,1),'r-')
plt.xlabel('height(cm)')
plt.ylabel('mass(kg)')
y_legend = "y="+str(round(beta[0],3))+"+"+str(round(beta[1],3))+"x"
plt.legend([y_legend,"observed-data"])
plt.title("Learning with Gradient Descent")
plt.show()
Stochastic Gradient Descent¶
ការធ្វើបរមាកម្មលើតម្លៃអនុគមន៍ដោយប្រើ Gradient Descent អាចជួយយើងឱ្យធ្វើការគណនា បានយ៉ាងមានប្រសិទ្ធភាពទោះបីជាវិមាត្រឬចំនួននៃអថេរពន្យល់ច្រើនក៏ដោយ។ ប៉ុន្តែក្នុងវិធីសាស្រ្ត Gradient Descent ការគណនា gradient ត្រូវបានធ្វើឡើងដោយប្រើប្រាស់ទិន្នន័យទាំងអស់ដែលមានក្នុងដៃ។ ក្នុងករណីដែលចំនួនទិន្នន័យមានច្រើន វិធីនេះត្រូវបានគេដឹងថាមានភាពយឺតយ៉ាវក្នុងការរួមទៅរកតម្លៃបរមារបស់អនុគមន៍។
ដើម្បីដោះស្រាយបញ្ហានេះ Stochastic Gradient Descent (SGD) ត្រូវបានប្រើប្រាស់ជំនួសវិញ។ ក្នុងករណីចំនួនទិន្នន័យដែលមាន(N) មានបរិមាណច្រើន ក្នុងវិធីSGD ទិន្នន័យម្តងមួយៗ ត្រូវបានជ្រើសយកដោយចៃដន្យដើម្បីគណនា gradient នៃអនុគមន៍ រួចធ្វើការផ្លាស់ប្តូរតម្លៃអថេរតែម្តង ដោយមិនចាំបាច់ធ្វើការបូកសរុបគ្រប់ទិន្នន័យដែលមាននោះឡើយ។
ជាទូទៅ ដើម្បីអនុវត្តSGDបាន ចំពោះទិន្នន័យសរុបDដែលមានអនុគមន៍ដែលត្រូវធ្វើបរមាកម្ម ត្រូវតែអាចសរសេរជាផលបូកនៃអនុគមន៍ដែលយកករណីទិន្នន័យនិមួយៗជាធាតុចូលដូចខាងក្រោម។
ក្នុងករណីយើងកំពុងសិក្សានេះ ដោយសារ\(E_D\left(\pmb{\beta}\right)\)ត្រូវបានកំណត់ដោយផលបូកការេនៃកម្រិតលម្អៀងគ្រប់ទិន្នន័យទាំងអស់ \(E_D\left(\pmb{\beta}\right)=\sum_{i=1}^{N}\epsilon_i^2\) ហេតុនេះ លក្ខខណ្ឌខាងលើត្រូវបានផ្ទៀងផ្ទាត់។
ចំពោះទិន្នន័យនិមួយៗ\(\left(\pmb{x}_i,y_i\right)\) gradient នៃអនុគមន៍ដែលត្រូវធ្វើបរមាកម្មអាចគណនាបានដូចខាងក្រោម។
កន្សោមសម្រាប់ធ្វើការផ្លាស់ប្តូរតម្លៃនៃអថេរតាម SGD គឺអាចបង្ហាញដូចទម្រង់ខាងក្រោម។
ដែល \(\pmb{\delta}_\pmb{i}=\left({{\hat{y}}_i}^{\left(t\right)}-y\right)\pmb{x}_i^\top\)។
ជាមួយPythonអ្នកអាចសរសេរCodeដូចខាងក្រោម។ នៅទីនេះយើងកំណត់យកតម្លៃចាប់ផ្តើមនៃ \(\pmb{\beta}^{\left(0\right)}=\mathbf{0}\ \) និង \(\eta=0.001\)
import random
beta = np.zeros(2)
d_index = list(range(len(X)))
eta = 1e-3
for t in range(100000):
random.shuffle(d_index)
for i in d_index :
XP = np.vstack([np.ones_like(X[i]), X[i]]).T
y_hat = XP @ beta
beta -= 2 * eta * XP.T @ (y_hat - y[i])
xa = np.linspace(1.45,1.72,50)
plt.scatter(X,y,marker='x')
plt.plot(xa,predict(xa,beta,1),'r-')
plt.xlabel('height(cm)')
plt.ylabel('mass(kg)')
y_legend = "y="+str(round(beta[0],3))+"+"+str(round(beta[1],3))+"x"
plt.legend([y_legend,"observed-data"])
plt.title("Learning with Gradient Descent")
plt.show()
បើយើងធ្វើការប្រៀបធៀបរវាង Gradient Descent និង SGD យើងអាចនិយាយបានថា SGD គឺជាវិធីសាស្រ្តដែលសន្មតយកតម្លៃ gradient ចំពោះគ្រប់ទិន្នន័យទាំងអស់ក្នុង Gradient Descent ដោយតម្លៃប្រហែល
\(\pmb{\delta}_\pmb{i}=\left({{\hat{y}}_i}^{\left(t\right)}-y\right)\pmb{x}_i^\top\ \) ពោលគឺ \( \frac{\partial E_D\left(\pmb{\beta}\right)}{\partial\pmb{\beta}}\approx\frac{\partial e_{\pmb{x}_i,y_i}\left(\pmb{\beta}\right)}{\partial\pmb{\beta}}=\pmb{\delta}_\pmb{i}\)។