.ipynb .pdf

Binder

Contents

ម៉ូឌែលតម្រែតម្រង់លីនេអ៊ែរ(១)

ការសិក្សាលើម៉ូឌែលនៃបាតុភូត អាចឱ្យគេរកឃើញពីមូលហេតុឬកត្តាទាក់ទងនៃបាតុភូតនោះបាន។លើសពីនេះគេក៏អាចប្រើប្រាស់ម៉ូឌែលនោះសម្រាប់ការទស្សន៍ទាយសម្រាប់អនាគតឬការប៉ាន់ស្មានលើទិន្នន័យដែលមិនមានក្នុងដៃ។

ជាទូទៅម៉ូឌែលដែលសិក្សាអំពីទំនាក់ទំនងរវាងលទ្ធផលនៃបាតុភូតមួយនិងកត្តាដែលអាចគិតបានថាជាកត្តាជះឥទ្ធិពលលើលទ្ធផលនោះ ហៅថា ម៉ូឌែលតម្រែតម្រង់ (Regression Model)។

ក្នុងផ្នែកនេះយើងនឹងសិក្សាអំពីម៉ូឌែលមានទម្រង់ជាលីនេអ៊ែរដែលជាមូលដ្ឋាននៃម៉ូឌែលតម្រែតម្រង់។

ការសិក្សាលើទំនាក់ទំនងរវាង២អថេរ

ជាឧទាហរណ៍យើងលើកយកការសិក្សារវាងទំនាក់ទំនងរវាងកម្ពស់(cm)និងម៉ាស(kg)តាមរយៈម៉ូឌែលតម្រែតម្រង់លីនេអ៊ែរ។

កម្ពស់(cm)	152	157	160	163	150	147	165	168	178
ម៉ាស(kg)	54.48	55.84	57.20	58.57	53.12	52.21	59.93	61.29	69.92

import matplotlib.pyplot as plt
import numpy as np
plt.ion()

X = np.array([152,157,160,163,150,147,165,168,170])
y = np.array([54.48,55.84,57.20,56.57,53.12,52.21,59.93,61.29,67.92])

plt.scatter(X,y,marker='x')
plt.xlim([145,172])
plt.ylim([50,70])
plt.xlabel('height(cm)')
plt.ylabel('mass(kg)')
plt.show()

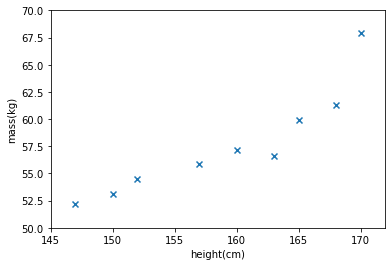
ក្នុងតារាងខាងលើ ទិន្ន័យអំពីកម្ពស់គិតជាសង់ទីម៉ែត្រ(cm)និងម៉ាសគិតជាគីឡូក្រាម(kg)របស់មនុស្ស៩នាក់។ ពីទិន្នន័យនេះ យើងចង់សិក្សាពីទំនាក់ទំនងរវាងកម្ពស់(x)និងម៉ាស(y)។ នៅទីនេះយើងសន្មតថា តម្លៃម៉ាស(\(y\))គឺជាអនុគមន៍នៃតម្លៃកម្ពស់(\(x\)): \(y=f(x)\)។ គោលដៅនៃចំណោទតម្រែតម្រង់គឺកំណត់អនុគមន៍ទំនាក់ទំនងនោះ។

ដើម្បីងាយស្រួល ជាដំបូងយើងឧបមាថាទំនាក់ទំនងរវាង \(x,y\) កំណត់ដោយអនុគមន៍ដឺក្រេទីមួយដូចខាងក្រោមដែលយើងហៅថា ម៉ូឌែលលីនេអ៊ែរ (Linear Model)។

\[ y=f(x)=\beta_0+\beta_1 x \]

ក្រោមសន្មតម៉ូឌែលបែបនេះទិន្នន័យដែលមានក្នុងតារាងត្រូវផ្ទៀងផ្ទាត់ទំនាក់ទំនងខាងលើនេះ។ ប៉ុន្តែក្នុងដំណើរការវាស់វែង ឬ ស្រង់ទិន្នន័យលម្អៀងឬគម្លាតរវាងតម្លៃតាមម៉ូឌែលដែលឧបមាខាងលើនិងតម្លៃទិន្នន័យជាក់ស្តែងតែងតែកើតឡើង។ ហេតុនេះ យើងសិក្សាករណីដូចខាងក្រោមដែល\(\epsilon\)ជាកម្រិតលម្អៀង។

\[ y_1 = \beta_0+\beta_1 x_1+\epsilon_1 \]

\[ y_2 = \beta_0+\beta_1 x_2+\epsilon_2 \]

\[ \vdots \]

\[ y_N = \beta_0+\beta_1 x_N+\epsilon_N \]

ក្នុងពេលនេះទិន្នន័យដែលមានអាចសរសេរជាទំនាក់ទំនងដូចខាងក្រោម។

\[ 54.58=\beta_0+\beta_1\times 152+\epsilon_1 \]

\[ 55.84=\beta_0+\beta_1\times 157+\epsilon_2 \]

\[ \vdots \]

\[ 69.92 = \beta_0+\beta_1\times 178+\epsilon_9 \]

xa = np.linspace(145,172,50)
w = np.array([-27.4,0.53])
plt.scatter(X,y,marker='x')
plt.plot(xa,w[0]+w[1]*xa,'g-')
for idx,i in enumerate(X):
    plt.plot([i,i],[y[idx],w[0]+w[1]*i],'-.',c='r',label='error')
plt.xlim([145,172])
plt.ylim([50,70])
plt.xlabel('height(cm)')
plt.ylabel('mass(kg)')
y_legend = "y=b+ax"
plt.legend([y_legend,"error"])
plt.show()

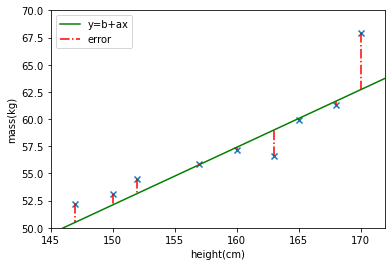
ជាទូទៅចំពោះទិន្នន័យចំនួន \(N: \{(x_i,y_i )\}_{i=1}^N\) ទិន្នន័យនិមួយៗអាចបង្ហាញដោយទំនាក់ទំនងដូចខាងក្រោម។

\[y_i=\beta_0+\beta_1 x_i+\epsilon_i (i=1,2,…,N)\]

នៅទីនេះ \(\beta_0 ,\beta_1\) ហៅថាមេគុណតម្រែតម្រង់(regression coefficient) \(\epsilon\) គឺតម្លៃលម្អៀងរវាងទិន្នន័យពីការវាស់វែងនិងតម្លៃតាមម៉ូឌែល។ តម្លៃនៃម៉ាស \(y\) ហៅថា អថេរគោលដៅ(subjective variable) \(x\) ហៅថា អថេរពន្យល់ឬអថេរឯករាជ្យ(explanatory variable)។

គោលដៅរបស់យើងនៅទីនេះគឺការកំណត់តម្លៃនៃមេគុណតម្រែតម្រង់ ដែលធ្វើអោយម៉ូឌែលដែលសន្មតខាងលើអាចបង្ហាញទំនាក់ទំនងរវាងអថេរពន្យល់និងអថេរគោលដៅបានល្អប្រសើរ។ មានវិធីជាច្រើនដែលអាចឱ្យយើងកំណត់តម្លៃនៃមេគុណតម្រែតម្រង់ដែលល្អប្រសើរសម្រាប់ទិន្នន័យដែលមាន។ នៅក្នុងអត្ថបទនេះ យើងនឹងណែនាំអំពីវិធីសាស្រ្តងាយនិងពេញនិយម Least Square Error ។

ការប៉ាន់ស្មានតម្លៃប៉ារ៉ាម៉ែត្រដោយLeast Square Error

តាមការសន្មតនៃម៉ូឌែលខាងលើ តម្លៃនៃលម្អៀងរវាងទិន្នន័យនិមួយៗនិងតម្លៃពិតតាមម៉ូឌែលអាច កំណត់បានដូចខាងក្រោម។

\[\epsilon_i=y_i-(\beta_0+\beta_1 x_i ) ,(i=1,2,…,N)\]

ក្នុងវិធីសាស្រ្តLeast Square Error យើងសិក្សាលើផលបូកនៃការេរបស់តម្លៃលម្អៀងទាំងអស់របស់ទិន្នន័យដែលមាន ពោលគឺ \(\epsilon_1^2+\epsilon_2^2+⋯+\epsilon_N^2\)។ គំនិតក្នុងវិធីសាស្រ្តនេះគឺងាយស្រួល។ម៉ូឌែលដែលអាចពន្យល់ទំនាក់ទំនងរវាងអថេរទាំង២បានល្អប្រសើរ អាចត្រូវបាននិយាយបានថាជាម៉ូឌែលដែលមានតម្លៃនៃកម្រិតលម្អៀងតូចបំផុត។ ហេតុនេះ យើងនឹងធ្វើការកំណត់តម្លៃមេគុណតម្រែតម្រង់(ប៉ារ៉ាម៉ែត្រ)ណាដែលធ្វើឱ្យតម្លៃនៃផលបូកនៃការេរបស់តម្លៃលម្អៀងទាំងអស់របស់ទិន្នន័យ \(E(\beta_0,\beta_1 )\)មានតម្លៃតូចបំផុត។

\[ E(\beta_0,\beta_1 )=\sum_{i=1}^{N}{\epsilon_i^2}=\sum_{i=1}^{N}{\left\{y_i-(\beta_0+\beta_1 x)\right\}^2} \]

អ្នកដែលបានសិក្សាគណិតវិទ្យា អាចមើលឃើញយ៉ាងងាយថា ពេលនេះវាបានក្លាយជាបញ្ហាបរមាកម្ម លើតម្លៃ \(E(\beta_0,\beta_1 )\) ដោយយក\(\beta_0,\beta_1\) ជាអថេរ។ យើងអាចដោះស្រាយបញ្ហានេះបានដោយងាយដោយប្រើចំណេះដឹងផ្នែកវិភាគមូលដ្ឋានដូចជាដេរីវេដោយផ្នែក។

នៅទីនេះ ដើម្បីមានភាពងាយស្រួលក្នុងការសិក្សាលើករណីច្រើនអថេរពន្យល់ យើងនឹងណែនាំការដោះស្រាយបញ្ហាខាងលើដោយប្រើវ៉ិចទ័រនិងម៉ាទ្រីស។ យើងកំណត់សរសេរម៉ាទ្រីសនិងវ៉ិចទ័រដូចខាងក្រោម។ \(X\) ពេលខ្លះត្រូវបានហៅថាម៉ាទ្រីសផែនការ។

\[\begin{split} X=\begin{pmatrix} 1 & x_1\\ \vdots & \vdots\\ 1 & x_N \end{pmatrix}\in \mathbb{R}^{N\times 2}, \pmb{y}=\begin{pmatrix} y_1\\ \vdots\\ y_N \end{pmatrix}\in \mathbb{R}^{N}, \pmb{\epsilon}=\begin{pmatrix} \epsilon_1\\ \vdots\\ \epsilon_N \end{pmatrix}\in \mathbb{R}^{N}, \pmb{\beta}=\begin{pmatrix} \beta_0\\ \beta_1 \end{pmatrix}\in \mathbb{R}^{2} \end{split}\]

ពេលនេះម៉ូឌែលនិងផលបូកតម្លៃការេនៃលម្អៀងខាងលើអាចសរសេរដូចខាងក្រោម។

\[ \pmb{y}=X\pmb{\beta}+\pmb{\epsilon} \]

\[ E(\pmb{\beta})=\sum_{i=1}^{N}{\epsilon_i^2}=(\pmb{y}-X\pmb{\beta})^{\top}(\pmb{y}-X\pmb{\beta}) \]

ត្រលប់ទៅកាន់បញ្ហារបស់យើងវិញ។ គោលដៅរបស់យើងគឺកំណត់តម្លៃ\(\pmb{\beta}\)ដែលធ្វើឱ្យតម្លៃនៃ \(E(\pmb{\beta})\) តូចបំផុត។ នៅទីនេះដូចដែលបានឃើញស្រាប់ អនុគមន៍ \(E(\pmb{\beta})\) ជាអនុគមន៍ប៉ោង ហេតុនេះយើងអាចកំណត់តម្លៃអប្បបរមារបស់វាបានងាយដោយគ្រាន់តែគណនាដេរីវេធៀបនឹងប៉ារ៉ាម៉ែត្រ\(\pmb{\beta}\)ដូចខាងក្រោម។

\[ E(\pmb{\beta})=(\pmb{y}-X\pmb{\beta})^\top\ (\pmb{y}-X\pmb{\beta})=\pmb{y}^\top\ \pmb{y}-2\pmb{y}^\top\ X\pmb{\beta}+\pmb{\beta}^\top\ X^\top\ X\pmb{\beta} \]

ដោយដោះស្រាយសមីការ \(\partial/\partial\pmb{\beta}\ E(\pmb{\beta})=-\mathbf{2}X^\top\ \pmb{y}-\mathbf{2}X^\top\ X\pmb{\beta}=\pmb{0}\) យើងបាន

\[ \hat{\pmb{\beta}}=(X^\top X)^{-1} X^T \pmb{y} \]

ដោយជំនួសតម្លៃដែលគណនាបាននេះទៅក្នុងម៉ូឌែលដើម យើងអាចគណនាតម្លៃទស្សន៍ទាយនៃអថេរគោលដៅ \(y\) នៅពេលស្គាល់តម្លៃអថេរពន្យល់ x បានដូចខាងក្រោម។

\[ \hat{\pmb{y}}=\pmb{x\hat{\beta}} \]

ក្នុងករណីទិន្នន័យក្នុងតារាងទី១ខាងលើ យើងអាចទទួលបានតម្លៃនៃមេគុណតម្រែតម្រង់និងបន្ទាត់តាងម៉ូឌែលតម្រែតម្រង់លីនេអ៊ែរដូចខាងក្រោម។

def fit(x,y,k):
  X_ = np.zeros((len(x),k+1))
  for i in range(k+1):
    X_[:,i] = x**i
  w = np.linalg.inv(X_.T@X_)@X_.T@y
  return w

def predict(x,w,k):
  X_ = np.zeros((len(x),k+1))
  for i in range(k+1):
    X_[:,i] = x**i
  return X_@w

w = fit(X,y,1)
xa = np.linspace(145,172,50)
plt.scatter(X,y,marker='x')
plt.plot(xa,predict(xa,w,1),'g-')
plt.xlim([145,172])
plt.ylim([50,70])
plt.xlabel('height(cm)')
plt.ylabel('mass(kg)')
y_legend = "y="+str(round(w[0],3))+"+"+str(round(w[1],3))+"x"
plt.legend([y_legend,"observed-data"])
plt.show()

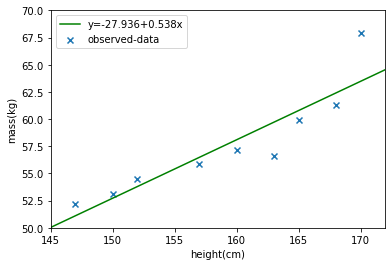
ឯករាជភាពនៃតម្លៃលម្អៀង Independence of errors

យើងពិនិត្យលើទំនាក់ទំនងរវាងតម្លៃនៃលម្អៀងនិងអថេរគោលដៅនិងអថេរពន្យល់។ បើសង្កេតលើតម្លៃនៃកូវ៉ារ្យង់រវាងតម្លៃលម្អៀង\(\epsilon\)និងតម្លៃទស្សន៍ទាយនៃអថេរគោលដៅ\(\hat{y}\) ឬ តម្លៃនៃកូវ៉ារ្យង់រវាងតម្លៃលម្អៀង\(\epsilon\) និងតម្លៃទស្សន៍ទាយនៃអថេរពន្យល់\(x\)យើងបានលទ្ធផលដូចខាងក្រោម។

(សម្រាយបញ្ជាក់ទុកជាលំហាត់សម្រាប់អ្នកអាន)

\[Cov\left[\hat{y},\hat{\epsilon}\right]=Cov\left[x,\hat{\epsilon}\right]=0\]

លទ្ធផលនេះបង្ហាញពីឯករាជភាពនៃតម្លៃលម្អៀងដែលបង្កើតដោយម៉ូឌែលនិងតម្លៃទស្សន៍ទាយនៃអថេរគោលដៅ ឬ អថេរពន្យល់។

Coefficient of determination \((\pmb{R}^\mathbf{2})\)

ដើម្បីបង្ហាញពីកម្រិតនៃការពន្យល់របស់ម៉ូឌែលទៅលើទំនាក់ទំនងរវាងទិន្នន័យដែលមាន Coefficient of determination \((\pmb{R}^\mathbf{2})\) ត្រូវបានប្រើ។ តម្លៃ \(\pmb{R}^\mathbf{2}\) កំណត់ដោយផលធៀបរវាង វ៉ារ្យង់នៃតម្លៃទស្សន៍ទាយរបស់អថេរគោលដៅ និង វ៉ារ្យង់នៃតម្លៃអថេរគោលដៅពិត។

\[ R^2=\frac{Var\left[\hat{y}\right]}{Var\left[y\right]}=1-\frac{Var\left[\hat{\epsilon}\right]}{Var\left[y\right]} \]

តម្លៃនេះយកតម្លៃលើចន្លោះ \(\left[0,1\right]\) ដែលតម្លៃខិតជិត១បង្ហាញពីភាពល្អប្រសើរនៃការពន្យល់របស់ម៉ូឌែលទៅលើទិន្នន័យ។

អំពីRegression ម៉ូឌែលតម្រែតម្រង់លីនេអ៊ែរ(២)